Enhancing Large Language Models with Localized Knowledge Bases
实践项目:用本地知识库强化大语言模型
摘要
本论文重点关注了当前大语言模型缺乏私域知识的问题,并实践了一种通过集成本地化知识库的方法来尝试解决该问题。为此,我们以重庆大学卓越工程师学院的专有信息搭建了开源大语言模型的本地知识库并进行评估。评估结果显示该方法大幅提高了大语言模型问答的准确性,同时减少了“幻觉”现象的发生,从而为大语言模型赋能增效。另外,本论文还尝试探讨了语言模型的演变及其应用,在追溯从统计语言模型到基于Transformer架构的语言模型发展历程的同时对大语言模型的内在机制进行阐释。本文将为大语言模型的行业应用以及可解释性人工智能等领域贡献独特视角,为未来更可靠、透明的AI系统的设计提供潜在价值。
Abstract
This thesis focuses on addressing the issue of insufficient domain-specific knowledge in current large language models (LLMs) by implementing an approach that integrates localized knowledge bases. To this end, we have constructed a localized knowledge base for an open-source large language model using exclusive information from Chongqing University’s Elite Institute of Engineering (EIE). Our evaluations show that this method significantly improves the accuracy of the LLM’s question-answering capabilities while reducing the occurrence of “hallucinations”, thus enhancing the power and efficiency of language models. Additionally, this thesis explores the evolution and application of language models, tracing the development from statistical language models to transformer-based architectures and elucidating the internal mechanisms of LLMs. This work offers unique perspectives for the industry application of LLMs and explainable AI, contributing to the design of more reliable and transparent AI systems in the future.
1. Introduction
1.1 Motivation
Large Language Models (LLMs) have significantly advanced natural language processing, demonstrating exceptional capabilities in generating complex and coherent text. At its core, a language model calculates the probability distribution of the upcoming sequences of words in a given context
Furthermore, to enhance the reasoning capabilities and accuracy of LLMs, we propose constructing a localized knowledge base. This innovation addresses the challenge of integrating domain-specific knowledge into LLMs, facilitating more accurate and contextually relevant responses. By developing such knowledge bases, we aim to create LLM-based digital avatars capable of engaging in meaningful interactions and responding to specific queries with greater precision.
This thesis aims to enhance the interpretability of LLMs by elucidating their intrinsic workings. Inspired by GPT-2’s architecture and recent theoretical frameworks
1.2 Thesis Structure
This thesis focuses on enhancing the transparency and effectiveness of LLMs by exploring mechanistic interpretability and integrating them with localized knowledge bases. Our experiments aim to develop a retrieval-augmented generation framework that improves LLMs’ accuracy and contextual relevance by dynamically incorporating domain-specific knowledge from Elite Institute of Engineering (EIE). The structure of this thesis can be listed as:
- In Chapter 2, we explore the evolution of language models from early statistical methods to sophisticated transformer-based architectures. This chapter highlights the research paradigms and significant technological advancements that have shaped modern language modeling.
- In Chapter 3, we discuss previous studies and methodologies that have influenced our approach, providing a critical analysis of current technologies and their limitations.
- In Chapter 4, we describe the methods and experimental setup used to integrate and test the effectiveness of localized knowledge bases within LLMs through the retrieval-augmented generation framework.
- In Chapter 5, we perform a thorough theoretical analysis of the internal mechanisms of LLMs, focusing on how they process and manage data. This analysis covers the dynamics of information flows and concept representations, providing insights into the mechanistic interpretability essential for explainable AI.
- In Chapter 6, we perform a thorough theoretical analysis of the internal mechanisms of LLMs, focusing on how they process and manage data. This analysis covers the dynamics of information flows and concept representations, providing insights into the mechanistic interpretability essential for explainable AI.
- In Chapter 7, we summarize the key findings and discuss the implications of this research for future studies. We outline the limitations encountered during the study and propose potential areas for further exploration to enhance the functionality and transparency of LLMs.
2. Background
The evolution of language models unfolds chronologically from the initial statistical language models (SLMs) to subsequent neural language models (NLMs), progressing to pre-trained language models (PLMs), and eventually to the current state of LLMs
The progression of language modeling evolve from statistical methods to neural network-based approaches, and subsequently to the transformer architecture and Generative Pre-trained Transformers (GPTs). This evolution of language model that we present here, has been driven by the need to capture the nuanced semantic meaning of language more effectively, thereby improving the performance of language modeling tasks. In this chapter, we present a new perspective on the developments of LLMs, contrasting with the traditionally chronological and exhaustively detailed view of LLMs
In this chapter, we will delve into the relentless pursuit of capturing nuanced semantic meaning via various kinds of language modeling methods, ranging from traditional $n$-gram models to the state-of-the-art architectures like GPT and Mamba. As each innovation builds upon the strengths of its predecessors while addressing their limitations, we can expect further advancements in language modeling to bring us closer to achieving human-level language understanding.
2.1 Early Statistical Models
Statistical Language Models (SLMs), which emerged prominently in the 1990s, are based on statistical learning methods that predict the likelihood of sequences in text. These models fundamentally rely on the Markov assumption, which assumes that the prediction of a word depends only on its predecessors, leading to the development of $n$-gram models (bigrams and trigrams are the most prevalent choices).
In order to construct the probability distribution $P(w_1 w_2 \dots w_n)$ for a word sequence $w_1,w_2,…, w_n$, which calculates the likelihood of the given word sequence appearing as a sentence $ \bigcup\limits_{i=1}^n w_i$, for example
Here we define $\mathbb{W}$ as the vocabulary of all words and $|\mathbb{W}|$ as the size of the vocabulary, $n$ is the number of words. Then, considering that sentence generation generally proceeds from left to right, the calculating process can be modeled as follows:
\[\begin{equation} \displaylines{ P\left(w_{1} w_{2} \ldots w_{n}\right)=P\left(w_{1}\right) P\left(w_{2} \mid w_{1}\right) P\left(w_{3} \mid w_{1} w_{2}\right) \cdot P\left(w_{n} \mid w_{1} w_{2} \ldots w_{n-1}\right) \\ =\prod_{i=1}^{n} P\left(w_{i} \mid w_{1} w_{2} w_{3} \ldots w_{n-1}\right)} \label{eq:2.2} \end{equation}\]For conciseness, Let \(\{ w_i \} _{i=1}^{n-1}\) denotes the sequence \(w_1,w_2,\ldots, w_{n-1}\), then
\[\begin{equation*} P\left(w_{1} w_{2} \ldots w_{n}\right)= \prod_{i=1}^{n} P\left(w_{i} \mid\left\{w_{i}\right\}_{i=1}^{n-1}\right) \end{equation*}\]The simplest approach to estimating \(\prod\limits_{i=1}^{n} P\left(w_{i} \mid\left\{w_{i}\right\}_{i=1}^{n-1}\right)\) based on a given corpora is to infer from the frequency of word sequences appearing in the corpora. Let $C(w_j)$ represent the count of a word sequence occurring in the corpora. By applying the principle of maximum likelihood estimation, when the sample size of words is sufficiently large, one can approximate the conditional probability between words using their relative frequencies, then:
\[\begin{equation} \prod_{i=1}^{n} P\left(w_{i} \mid\left\{w_{i}\right\}_{i=1}^{n-1}\right)=\frac{C\left(w_{1} w_{2} w_{3} \ldots w_{i-1} w_{i}\right)}{C\left(w_{1} w_{2} w_{3} \ldots w_{i-1}\right)} \label{eq:2.3} \end{equation}\]To address issues of data sparsity inherent in high-order $n$-grams, various smoothing techniques were introduced, like backoff estimation and Good–Turing estimation. Backoff estimation allows for a graceful degradation of $n$-gram order when data is insufficient, while Good–Turing estimation adjusts the probability distribution to better account for unseen events in a dataset.
SLMs have been critical in advancing the performance of various NLP tasks, and they are especially adept at handling relatively small corpora. However, they were constrained by the curse of dimensionality, as the number of possible word sequences increases exponentially with the length of the context window
Moreover, SLMs faced limitations in handling the complexity and variability of human languages
2.2 Paradigm Shift to Neural Network Models
The transition from Statistical Language Models (SLMs) to Neural Language Models (NLMs) marked a significant paradigm shift in natural language processing. While SLMs generate word sequences using probability distributions, NLMs leverage the power of neural networks to capture complex language representations.
The pioneering work
Multilayer Percpetrons (MLP). MLPs are feed-forward neural networks consisting of an input layer, one or more hidden layers, and an output layer. In the context of language modeling, MLPs take a fixed-size context window of words as input and predict the next word in the sequence.
For an MLP with $L$ hidden layers, the activation of the $l$-th layer, $\mathbf{h}^{(l)}$ can be expressed as:
\[\begin{equation} \boldsymbol{h}^{(l)}=\sigma\left(\boldsymbol{W}^{(l)} \boldsymbol{h}^{(l-1)}+\boldsymbol{b}^{(l)}\right) \label{eq:2.4} \end{equation}\]where $\mathbf{W}^{(l)}$ and $\mathbf{b}^{(l)}$ are the weight matrix and bias vector of the $l$-th layer, respectively, and $\sigma(\cdot)$ is a non-linear activation function, such as $\tanh$ or sigmoid. MLPs are trained using the back-propagation algorithm which is based on gradient descent optimization of a loss function:
\[\begin{equation} \mathcal{L}(\Theta)=-\log P(y \mid \boldsymbol{x} ; \Theta) \end{equation}\]where $\Theta$ represents all the learnable parameters of the MLP. MLPs have limitations in capturing long-range dependencies due to the fixed-size context window and lack of explicit memory mechanisms, but they laid the foundation for more advanced neural network architectures, such as RNN.
Recurrent Neural Networks (RNN). RNNs are a class of neural networks designed to process sequential data. Unlike MLPs, RNNs maintain a hidden state that serves as a memory, allowing them to capture long-term dependencies in language. RNNs addressed the sequential nature of language by maintaining a hidden state \(\mathbf{h}_{t}\) that depends on the current input \(\mathbf{x}_{t}\) and the previous hidden state \(\mathbf{h}_{t-1}\):
\[\begin{equation} \boldsymbol{h}_{t}=\sigma\left(\boldsymbol{W}_{h h} \boldsymbol{h}_{t-1}+\boldsymbol{W}_{x h} \boldsymbol{x}_{t}+\boldsymbol{b}_{h}\right) \end{equation}\]where \(\boldsymbol{W}_{h h}\), \(\boldsymbol{W}_{x h}\) and \(\boldsymbol{b}_{ h}\) are are all learnable parameters, and $\sigma(·)$ is a non-linear activation function.
RNNs have shown remarkable success in various natural language processing tasks because of their recurrent structure, including language modeling, machine translation, sentiment analysis, etc. However, standard RNNs suffer from the vanishing gradient problem, which hinders their ability to capture long-range dependencies effectively. To address this issue, variants of RNNs, such as Long Short-Term Memory (LSTM)
Long Short-term Memory (LSTM). However, training RNNs for tasks that require long-range information proved challenging due to the vanishing gradient problem. LSTM networks
where \(\mathbf{i}_{t}\), \(\mathbf{f}_{t}\) and \(\mathbf{o}_{t}\) are the input, forget, and output gates, respectively, and \(\mathbf{c}_{t}\) is the cell state, and \(\odot(\cdot)\) here denotes element-wise multiplication. LSTMs became the most commonly used extension to RNNs for language modeling tasks.
2.3 Emergence of the Generative Pre-trained Transformer
The introduction of the transformer architecture by researchers at Google
Given an input sequence \(\boldsymbol{X} = \{\mathbf{x}_{1}, \ldots, \mathbf{x}_{n}\}\), the self-attention mechanism computes query, key, and value matrices \(\boldsymbol{Q}, \mathbf{K}\) and \(\boldsymbol{V}\) by using learned projection matrices \(\boldsymbol{W}_{Q}\), \(\boldsymbol{W}_{K}\) and \(\boldsymbol{W}_{V}\). The attention scores are computed as the scaled dot product between the query and key matrices, followed by a \(\text{softmax}\) function to obtain attention weights:
\[\begin{equation} \begin{aligned} \boldsymbol{Q}=\boldsymbol{X}^{T} \boldsymbol{W}_{Q} \quad \boldsymbol{K}=\boldsymbol{X}^{T} \boldsymbol{W}_{K} \quad \boldsymbol{V}=\boldsymbol{X}^{T} \boldsymbol{W}_{V} \\ \operatorname{Attention}(\boldsymbol{Q}, \boldsymbol{K}, \boldsymbol{V})=\operatorname{softmax}\left(\frac{\boldsymbol{Q} \boldsymbol{K}^{T}}{\sqrt{d_{k}}}\right) \boldsymbol{V} \end{aligned} \end{equation}\]where $d_k$ is the dimension of the key vectors. Multi-head attention extends this mechanism by performing self-attention in parallel across multiple heads, allowing the model to capture different aspects of the input sequence.
The Generative Pre-Trained Transformer (GPT) model, introduced by OpenAI
In summary, the emergence of transformer architectures and the subsequent development of PLMs have revolutionized the field of natural language processing, enabling significant advancements in a wide range of language-related tasks, from machine translation and sentiment analysis to question-answering and text generation, and so forth. By training on vast amounts of unlabeled text data, PLMs learn rich representations of language that can be fine-tuned for various downstream tasks.
2.4 The Stage of Large Language Models
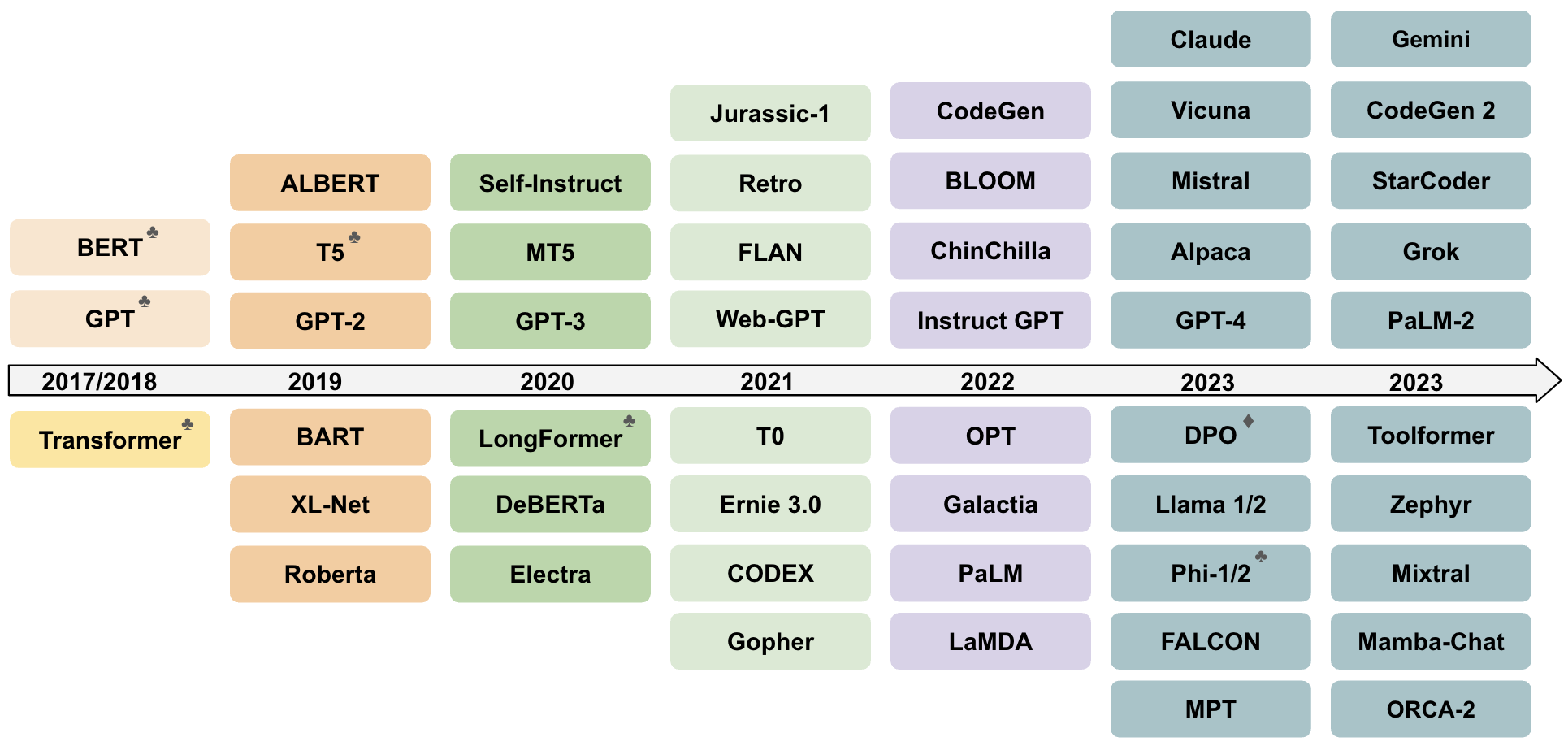
Over extensive research spanning decades, language modeling has progressed from initial SLMs to the contemporary landscape of LLMs. LLMs, the large-sized PLMs, show unprecedentedly emergent abilities that go beyond traditional language modeling and start to gain capability to solve more general and complex tasks that was not seen in PLM. The remarkable examples are such as GPT-4
Data Processing. As shown in Chapter 2, the evolution of language models highlights the importance of abundant, heterogeneous and high-scored mixture of data, necessitating the process for data.
-
data collection: As “garbage in, garbage out” suggests, the input data for training or tuning an LLM has a direct impact on the quality of the derived model. The pursuits for data processing
are good quality, proper diversity and large amounts. Thus the collection of diverse data, including texts from websites, academic papers, codes, and so on, demands a diverse range of data formats. -
data cleaning: Cleaning involves identifying and correcting inaccurate and redundant elements within the raw data, such as eliminating duplicated or erroneous data, and reducing noise. Furthermore, some filtering approaches should be applied to minimize the presence of irrelevant or biased information. Moreover, safeguarding privacy is essential; therefore, personal details like names, addresses, and phone numbers should be carefully removed from the dataset before training.
-
tokenization: Analogous to the cognitive mechanisms of the human brain, languages typically simplify complex units into chunks, and in the field of NLP, the chunks are often referred to as tokens through the process known as tokenization. Historically, NLP began with word-level tokenization, using spaces and punctuation to delineate words. The trajectory of semantic representation development has progressed from the Bag-of-Words model to more sophisticated approaches, such as Word2Vec
and GloVe , all of which aim to capture semantic representations at the word level. Tokenization breaks texts down to smaller units, which can be words, subwords, or symbols. Tokenization helps LLMs to handle out-of-vocabulary words by breaking them down into subwords, which enhances the model’s adaptability.
Training. The training process for LLMs consists of two main stages: unsupervised pre-training and supervised fine-tuning.
-
unsupervised pre-training: During pre-training, LLMs are exposed to the large corpora of data, learning the underlying structure of the language without any task-specific instructions. This stage allowed the model to develop the almost all broad knowledge of language, including semantics and pragmatics, as the superficial alignment hypothesis suggests
. -
instruction tuning: During instruction tuning, LLMs are trained by instruction-output pairs
to enhance their capabilities, which come from human instructions and desired outputs respectively. The instruction tuning process constricts the outputs from LLMs under the desired responses, allowing human to intervene with the models’ behaviors. -
fine-tuning: LLMs are refined and aligned with human values during the fine-tuning stage, through specific tasks, such as translation, question-answering, and summarization, which are trained on smaller, task-specific datasets.
Components. The following paragraphs briefly introduce each component. For in-depth mathematical analysis, please refer to Chapter 5 for detailed descriptions:
-
multi-head masked self-attention mechanism: This attention mechanism allows a model to weigh the importance of different words in a sentence. Unlike previous models such as RNN or LSTM that process words in a sequential manner, self-attention enables the model to look at all parts of the sentence simultaneously. This allows for a more nuanced understanding of context and relationships between words, regardless of their position in the sentence. The masking operation is a critical aspect of this mechanism, especially in the context of language modeling, which ensures that the prediction of a current word does not get influenced by future words.The reason for using the masked version of multi-head attention for the output embeddings is that when we are generating the output text, we do not have the next words yet because the next words are not generated yet
. -
layer normalization and residual connections: Each transformer block in GPT includes layer normalization and residual connections. Layer normalization is applied after the self-attention mechanism and after the feed-forward network within each transformer block. It normalizes the inputs across the features, improving the stability of the model. Residual connections allow the input of each sub-layer (i.e., the self-attention and feed-forward networks) to be added to its output.
-
position-wise fully connected feed-forward network: In each transformer block in GPT, after the attention mechanism together with corresponding layer normalization and residual connection, the output is passed through a feed-forward network that applies the same transformation to each position separately and identically.
-
positional encoding: Considering transformers do not inherently process sequential data in order, they use positional encodings to incorporate information about the order of the sequence into their inputs, e.g. RoPE from @Su2021. These positional encodings are added to the input embeddings at the bottom of the model stack, providing the model with information about the position of each word in the sequence.
Limitations. LLMs encounter a lot of challenges, including hallucinations, outdated or insufficient knowledge, memory issues, highly abstract reasoning tasks, mimicking human-like cognition,and much more
-
Hallucination: The phenomenon of hallucination occurs when LLMs generate misleading or outright incorrect outputs. These errors often stem from the LLMs’ lack of real-world knowledge, biases in training data, incomplete or false information, over-fitting during training, quantization errors, and the absence of relevant contextual background in prompts, etc. In summary, despite their vast number of parameters, LLMs capture only a small fraction of real-world knowledge and are limited by the temporal scope of their training data. Hallucination raises concerns over the reliability and usefulness of LLMs in real-world applications. For example, when working with patient records and medical data, hallucinations have critical consequences.
-
Fairness: LLMs tend to inherit social prejudices from their training data, which significantly impact their fairness in tabular prediction and question-answering tasks, which is hard to mitigate through prompt engineering process. Fairness and bias mitigation techniques encompass pre-processing, in-training, intra-processing, and post-processing interventions
. -
Political bias: Understanding the bias within language models is complicated due to the contextual and cultural factors. The LLMs ideology injection experiments
validate that LLM is indeed susceptible to ideologizing, as it exhibited notable emotional deviations particularly on sensitive topics, and that ChatGPT tends to exhibit a preference for left-leaning and pro-environmental viewpoints in its responses to questions.
Bias mitigation
2.5 Trends in Language Modeling
In this part, we explore some significant trends in language modeling, focusing on pre-training, emergent abilities, scaling laws, and the move towards more efficient models. Pre-training enhances LLMs’ adaptability and transfer learning. Emergent abilities like in-context learning and multi-step reasoning enable complex task completion. Scaling laws show how increasing model size, dataset size, and computational resources improve performance. A new trend highlights that smaller, efficient models can achieve high performance, challenging the belief that bigger is always better.
Pre-training. These large-scale models demonstrate unique behaviors in tasks such as zero-shot learning, which were previously challenging for smaller-scale models. The notion of pre-training in this context refers to the process by which these models acquire a general understanding of language from vast corpora.
Unlike traditional methods that often start from scratch, pre-training allows models to build upon an expansive, pre-existing linguistic framework. This approach not only enhances the efficiency of the learning process but also enables effective transfer learning. The knowledge acquired during pre-training can be applied to tasks well beyond those it was originally trained on, demonstrating the model’s adaptability and the broad applicability of its learned features.
This trend towards larger, more capable LLMs underscores a critical shift in NLP research and development, moving from narrowly focused models to versatile, highly capable systems that can understand and interact in human-like ways across multiple languages and tasks. As we continue to push the boundaries of what these sophisticated models can achieve, the role of pre-training in achieving state-of-the-art results in NLP becomes increasingly prominent, setting the stage for future innovations in the field.
Emergent abilities of LLMs. Recent research has revealed emergent abilities of LLMs, such as improved performance on few-shot prompted tasks
The GPT-3 model
Scaling Laws. Scaling the size of the architectures and the amount of training data has enabled unprecedented capabilities for the resulting LLMs, eliminating the need for fine-tuning on specific tasks. Scaling the size of the architectures and the amount of training data enabled unprecedented emergent capabilities for the resulting LLMs, eliminating the need for fine-tuning for specific tasks. From Kaplan’s insight
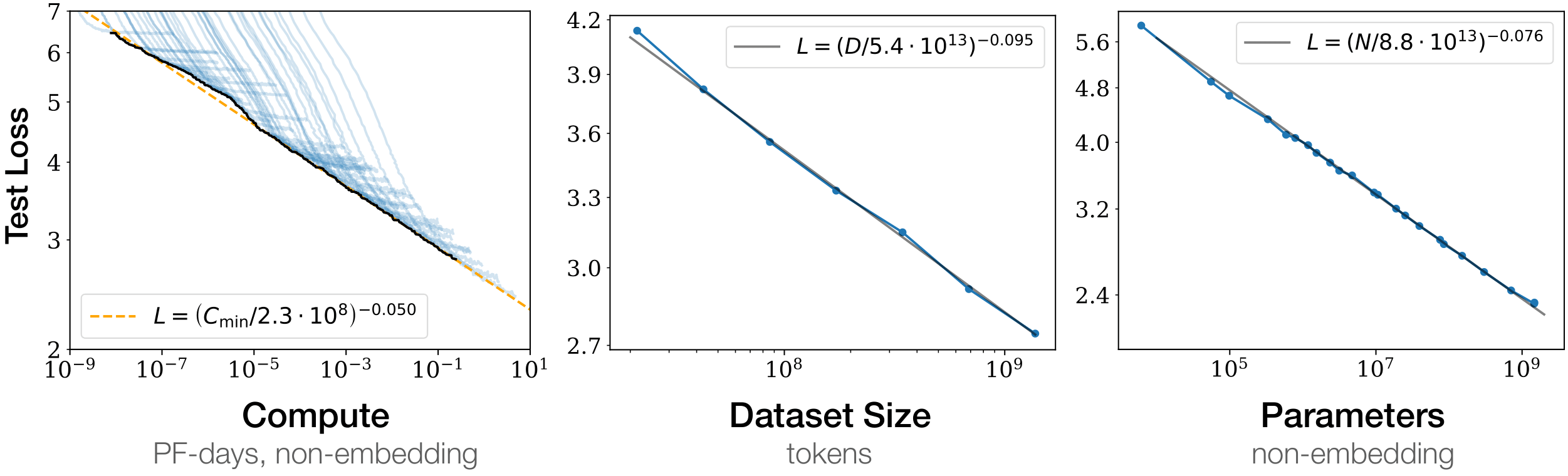
Let $P$ denote the model size (number of parameters) and $D$ denote the dataset size (number of tokens in the corpora). According to the empirical formula
Less But More. While the prevailing pursuit has been the ever-increasing model sizes, which leads to the growth of parameters from millions to billions and now trillions. A compelling counter-narrative is emerging. The new trend aims at reducing model size while maintaining or even enhancing language models’ performances, as exemplified by works such as ChatGLM-6B
Recent studies
3. Related Works
Transformer Circuits:
The residual stream captures the semantic and contextual knowledge that has been distilled from the input, facilitating the model’s ability to learn and reason about complex linguistic patterns.
According to researchers
The study of transformer circuits involves analyzing how individual components, such as attention heads and feed-forward layers, interact within these circuits to perform complex tasks. In summary, the concept of transformer circuits, provides a framework for understanding the internal mechanisms of transformers.
Understanding Internal Representations:
Recent studies have focused on the inner workings of concept representation of LLMs, revealing intriguing patterns of knowledge storage inside them. In 2017, OpenAI’s discovery of the sentiment neurons
Further research has led to the identification of other types of neurons, including polysemantic neurons
Notably, the superposition hypothesis
The idea that linguistic concepts are represented in a vector space within LLMs aligns with the linear representation hypothesis, where high-level concepts are represented linearly as directions in their representation space
Retrieval-Augmented Generation.
With the rapid development of LLMs, Retrieval-Augmented Generation (RAG) has become a predominant method in the field of professional knowledge-based question answering, which becomes the popular approach to equip LLM with domain knowledge. RAG framework answers a question in four steps: the user proposes a query, the system retrieves the relevant content from private knowledge bases, combines it with the user query as context, and finally asks the LLM to generate an answer. This process mirrors the typical cognitive process of encountering a problem, including consulting relevant references and subsequently deriving an answer. In this framework, the pivotal component is the accurate retrieval of pertinent information, which is critical for the efficacy of the RAG model.
Most professional documents are mainly stored in PDFs, the low accuracy of PDF parsing significantly impacts the effectiveness of professional knowledge-based question-answering . The process of retrieval from PDF files is fraught with challenges
Gaps in Current Research:
While significant advancements have been made in understanding and enhancing LLMs, several gaps remain. Current models often lack transparency, and the integration of domain-specific knowledge is still in its nascent stages. This thesis aims to address these gaps by developing a retrieval-augmented generation framework that integrates localized knowledge bases with LLMs. By doing so, it seeks to improve the interpretability and contextual relevance of LLMs, making them more reliable and effective for specialized applications.
4. Methodology
This chapter presents our proposed retrieval-augmented generation (RAG)
4.1 Experimental Approach
Retrieval-Augmented Generation. The RAG technique allows for dynamic updating and refinement of information in vector databases, rendering it exceptionally beneficial in disciplines requiring nuanced and evolving datasets such as history, medical sciences, and law. The strategic integration of LLMs with vector databases significantly augments their capabilities. This integration empowers LLMs to deliver responses that are not only accurate but also tailored to specific domains and sensitive to the temporal aspects of queries. The RAG approach underpins a novel paradigm in data retrieval and generation by combining domain-specific, timely data retrieval with contextually aware response generation.

From Fig 4.1 we can tell that the RAG framework boosts the efficacy of LLMs through two key components: retrieval and generation.
- By retrieving relevant documents from a specialized knowledge base, and secondly, by synthesizing this information into coherent, contextually enriched responses. The retrieval component, typically a sophisticated neural network, is adept at sifting through extensive databases to fetch documents that are most relevant to the input query.
- The generative component, on the other hand, seamlessly weaves this fetched information into the output generated by the LLM, thereby significantly enhancing both the accuracy and relevance of its responses. This integration allows LLMs to perform with heightened factual accuracy and situational appropriateness, particularly for queries that are domain-specific and time-sensitive.
Digital Avatars:
The RAG approach provides a compelling framework for the establishment of specialized knowledge bases in academic settings. A notable example of this is the development of a private domain knowledge base for the National Elite Institute of Engineering (EIE) at Chongqing University. Founded in September 2022, EIE aspires to cultivate exemplary future engineers and lead innovative practices in new engineering education. The institute’s unique curriculum and research focus are not naturally embedded within the pre-existing data of LLMs, necessitating the creation of an LLM-based digital avatar to address this gap.
This digital avatar is designed to field a wide array of inquiries pertaining to the institute, covering aspects such as the academic programs, faculty qualifications, enrollment processes, campus lifestyle, and extracurricular activities. To effectively fulfil this role, the digital avatar’s underlying LLM needs to be enriched with comprehensive, domain-specific information about EIE. Given the sensitive nature of some of this information, and considering future scalability and potential commercial applications, an open-source and domestic language model is preferable. Therefore, we have opted for ChatGLM3 as the operational core of our digital avatars.
ChatGLM3:
ChatGLM3 is a generation of pre-trained dialogue models jointly released by Zhipu AI and Tsinghua KEG. ChatGLM3-6B is the open-source model in the ChatGLM3 series, maintaining many excellent features of the first two generations such as smooth dialogue and low deployment threshold, while introducing the following features:
-
Stronger Base Model: The base model of ChatGLM3-6B, ChatGLM3-6B-Base, adopts a more diverse training dataset, more sufficient training steps, and a more reasonable training strategy. Evaluations of datasets from various perspectives such as semantics, mathematics, reasoning, code, and knowledge show that ChatGLM3-6B-Base has the strongest performance among base models below 10B.
-
More Complete Function Support: ChatGLM3-6B adopts a newly designed Prompt format, supporting multi-turn dialogues as usual. It also natively supports tool invocation (Function Call), code execution (Code Interpreter), and Agent tasks in complex scenarios.
-
More Comprehensive Open-source Series: In addition to the dialogue model ChatGLM3-6B, the basic model ChatGLM3-6B-Base, the long-text dialogue model ChatGLM3-6B-32K and further strengthens the ability to understand long texts ChatGLM3-6B-128K have also been open-sourced. All these weights are fully open for academic research, and free commercial use is also allowed after registration via a questionnaire. and intelligent systems in the realm of artificial intelligence.
LangChain-Chatchat:
LangChain-Chatchat is an open-source project that aims to implement a knowledge and search engine-based question-answering (Q&A) system using the LangChain framework and either open-source or remote LLMs’ APIs. The primary goal is to build a Q&A solution that is friendly to Chinese scenarios, supports open-source models, and can run both offline and online. The key features and benefits are listed below:
-
localized knowledge base: LangChain-Chatchat enables the creation of a local knowledge base Q&A application, ensuring data privacy and security for businesses.
-
flexible model support: The project supports various open-source LLMs and Embedding models, such as Vicuna, Alpaca, LLaMA, Koala, and RWKV, through the integration with FastChat. It also allows the use of remote APIs like OpenAI GPT and Zhipu API.
-
offline and online deployment: With the help of open-source LLMs and Embedding models, LangChain-Chatchat can be fully deployed offline, ensuring data privacy. It also supports online deployment through FastAPI and Streamlit WebUI.
-
extensible architecture: The project is designed to be easily extensible, allowing for the integration of additional models and remote APIs in the future.
-
open-source and free: LangChain-Chatchat is released under the Apache License, making it free for commercial use without any fees.
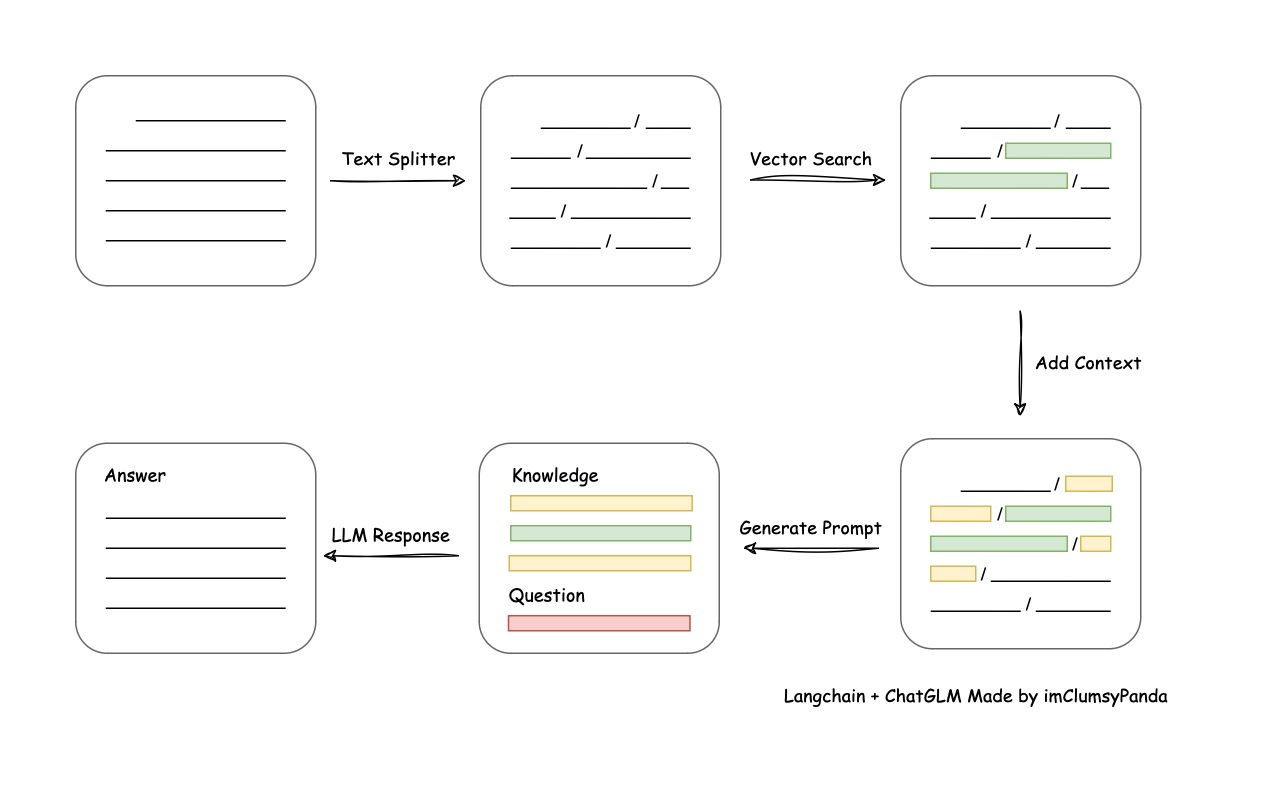
The main process of LangChain-Chatchat as Fig 4.2 indicates:
- Loading files and reading text
- Text segmentation and vectorization
- Question vectorization
- Matching the top-k most similar text vectors to the question vector
- Adding the matched text as context to the prompt along with the question
- Submitting the prompt to the LLM to generate an answer
Knowledge poisoning attacks:
In this thesis, we also explore malicious knowledge injection or knowledge poisoning attacks on LLMs. We intentionally supplied ChatGLM3 with incorrect or biased information, termed poisoned knowledge, and observed the reactions of the language model. Knowledge poisoning attacks involve deliberately injecting harmful or misleading information into the knowledge base that an LLM relies on. This can be particularly problematic in frameworks like RAG, where the LLM retrieves and integrates information from a large database to generate responses. By contaminating this knowledge base with biased or false information, attackers can manipulate the model’s output, causing it to produce incorrect, biased, or harmful responses.
4.2 Implementation Details
Data collection and preprocessing:
As we fully discussed before, the RAG framework can be utilized to create domain-specific knowledge bases. In this section, we begin to build the RAG-based EIE knowledge base with the help of LangChain-Chatchat, aiming to construct an enhancing tool for our digital avatar project. The LLM is enriched with information relevant to EIE, and thus we need to collect data in Markdown format to construct our corpora.
Our curated corpus includes a brief introduction to EIE, party building work, student activities in 2024, laboratory construction, campus life, and curriculum. Although directly uploading documents when loading knowledge base files can achieve basic question answering, the effect cannot be maximized. Therefore, we performed preprocessing work on the Markdown files, which includes:
- Formatting text or PDF documents according to the Markdown format.
- Typesetting the key points of the documents in Markdown format.
- Placing duplicate content files under the same topic file to facilitate the retrieval process of RAG and increase the probability of LLMs retrieving desired answers.
- Simplifying ambiguous sentences or long, difficult sentences in the knowledge base to avoid statements that can easily cause misunderstandings by LLMs, reducing the probability of LLM answering errors due to retrieving ambiguous sentences.
- Deleting special symbols or redundant information to facilitate the text vectorization process.
Experience has shown that the modified Markdown files have a higher recall rate and better answering effect when embedded in the LLMs’ knowledge base. The preprocessing steps ensure that the knowledge base is well-structured, concise, and free from ambiguity, thereby improving the overall performance of the RAG-based EIE knowledge base in the digital avatar project.
By following these guidelines and leveraging the power of the RAG framework, we create a robust and efficient knowledge base that enhances the capabilities of our digital avatar.
Chunking strategy:
Chunking is a critical preprocessing step in corpora’s embedding process, where large texts are segmented into manageable pieces that better align with user queries in semantic search applications. Effective chunking ensures that each piece is semantically cohesive, minimizing dependencies on the surrounding context, which enhances the retrieval accuracy. The challenge lies in determining the optimal chunk size; too large or too small can lead to imprecise search results or missed opportunities to display relevant information. This process directly impacts the quality of information retrieval by ensuring that search results closely match the query’s intent, thus addressing user needs more precisely.
Vectorization and Database Indexing with Faiss:
After chunking, text data undergoes vectorization, converting it into numerical vector matrices. Our implementation uses FlagEmbedding
Faiss
Vectors are indexed and stored in a vector database system tailored for RAG applications. We chose Faiss for its efficiency in similarity search and clustering of dense vectors, which is crucial for managing extensive datasets typical in applications. Faiss supports $L 2$-normalization and cosine similarities and is optimized for both CPU and GPU environments, ensuring efficient data handling. Incorporating Faiss provides advanced indexing and search capabilities, offering a robust solution for vector database management and significantly improving our RAG system’s performance.
Design of prompt templates:
The design of prompt templates is crucial in influencing the accuracy of model outputs in RAG scenarios. Effective prompts typically include task descriptions, background knowledge retrieved from databases, and specific user queries. Our experimental findings suggest that the art of prompt design is often reliant on personal experience, lacking a definitive methodological framework. Consequently, prompts require continuous optimization based on the model’s real-time outputs to enhance their effectiveness.
Markdown format:
To optimize the utilization of the comprehensive knowledge base specific to the National Elite Institute of Engineering (EIE), which includes data on academic curricula, faculty research interests, laboratory resources, and industrial partnerships, we have adopted the Markdown format. This relatively rich database not only informs the LLMs but also ensures the outputs are factually accurate and contextually relevant. Given the clarity, readability, and structural organization afforded by Markdown, it facilitates and enhances information retrieval, making it a suitable choice for formatting.
Markdown is a lightweight markup language designed to format plain text using a simple syntax. It is widely used for creating structured documents on platforms such as GitHub, Jupyter notebooks, and various content management systems. When feeding data into our case, using markdown format provides several benefits:
-
structured and rich content: Markdown enables the organization of information into headings, lists, tables, and other structured elements, aiding in the preservation of context and ease of understanding. Moreover, Markdown supports basic formatting options like bold, italics, links, and code blocks, Markdown enriches the context provided to the language model.
-
embedding links and references: The ability to embed hyperlinks, footnotes, and references in Markdown is crucial in RAG scenarios, as it allows for referencing external sources or including additional contextual details.
-
ease of authoring: Markdown is not only human-readable but also straightforward to author, allowing content creators to efficiently produce well-structured documents without the need for complex formatting tools.
-
chunking: In RAG systems, chunking—otherwise known as the process of breaking down extensive documents—makes the data more manageable and processable.
Summarization:
In summary, the integration of localized knowledge bases with LLMs aims to address the challenges associated with the “black box” nature of these models. The primary objective of this thesis is to enhance the mechanistic interpretability of LLMs by integrating them with localized knowledge bases. The conceptual framework for this integration is rooted in the development and implementation of a RAG framework. This model leverages both the generative capabilities of LLMs and the precise information retrieval from knowledge bases to produce contextually relevant and accurate outputs.
5. Theoretical Analysis
In this chapter, we delve into the mathematical analysis underlying transformer architectures, exploring the internal residual stream and representation space, and therefore provide a simplified mathematical summary of the intrinsic workings of LLMs.
5.1 Mathematical Models and Mechanistic Interpretability

Mechanistic interpretability
Autoregressive models predict subsequent tokens based solely on preceding ones, followed by a decoder-only architecture. This architecture uses the self-attention based mechanism, to process the input sequences through a series of multiple transformer layers, where each layer applies masked multi-head self-attention followed by a fully connected feed-forward network, capturing long-range dependencies and producing coherent output tokens. Readers may refer to Figure 5.1 for an illustrative and intuitive understanding.
The internal state of the transformer, known as the residual stream, is the summation of the outputs from all preceding components
| At first, we define shorthand notation \(\left\{s_{(i)}\right\}_{i=1}^{n}\) to denote sequence, and as for each \(\left\{s_{(i)}\right\}_{i=1}^{n}\) in set \(S\), we use \(S^\star := \bigcup\limits_{n \in \mathbb{N}} S^n\) to denote the set of sequences with arbitrary length \(n\in \mathbb{N}\) , and $$ | S | $$ as the length of the set $S$. Notice that in practical settings, though sequences can theoretically extend indefinitely, a maximum context length is imposed by computational constraints. Further, we here define mapping $\mathcal{F}^\star:S_1^\star \rightarrow S_2^\star$ to represent an entrywise function: |
Tokenization $\mathcal{K}$. The sequences of characters \(\left\{a_{(i)}\right\}_{i=1}^{p}\) from a given alphabet $\mathbb{A}$ form a specific word. We here define the injective mapping \(\mathcal{K}^{\star}: \mathbb{A}^{\star} \rightarrow \mathbb{T}^{\star}\), which maps the input texts to a sequence of tokens defined by \(\left\{t_{(i)}\right\}_{i=1}^{q}\), and typically \(\mathbb{T}:=\{1,2, \ldots,|\mathbb{T}|\}\). The process of tokenization encodes each subword \(a_{i}\) individually, which is then mapped as tokens and thus the input sequence henceforth segmented. For instance, the tokenizer of GPT-4 splits the term “cohomology” into the subwords: “co” (prefix), “hom”, and “ology” (suffix).
While these methods provide a convenient way to segment text, they do not capture the underlying semantic information. Popular subword tokenization methods, such as byte pair encoding
Embedding \(\mathcal{E}\). To enable neural networks to effectively process and learn from the complex linguistic data, token sequences \(\left\{t_{(i)}\right\}_{i=1}^{q}\) are then embedded into a high dimensional Euclidean space \(\mathbb{E}:=\mathbb{R}^{d}\) through dense vector representations. Formally, the embedding function \(\mathcal{E}:\mathbb{T} \rightarrow \mathbb{E}\) maps each token \(t_{(i)}\) from the token vocabulary \(\mathbb{T}\) to a $d$-dimensional dense vector \(\boldsymbol{e}_{(j)}\), such that norm \(\left\|\mathcal{E}\left(t_{\alpha}\right)-\mathcal{E}\left(t_{\beta}\right)\right\|\) corresponds to the linguistic similarity of the subwords represented by the tokens \(t_{\alpha}\) and \(t_{\beta}\).
These embedded vectors \(\left\{\boldsymbol{e}_{(j)}\right\}_{j=1}^{r}\) are stored in a matrix \(\boldsymbol{E}\), which \(\in \mathbb{R}^{\|\mathbb{T}\| \times d}\), where each row represents the embedding of a specific token. The most famous example
The goal of embedding is to represent linguistic similarity between subwords through the distance between their corresponding embedding vectors, and Euclidean space makes it compatible with a wide range of linear algebraic operations. This approach, as opposed to one-hot encoding, where each word would be represented as a sparse vector of size \(\|\mathbb{T}\|\) with all zeros except for one element, results in capable of representing the various aspects of word relationships, both monolingual
Positional Encoding \(\mathcal{P}\). Since the embeddings \(\mathcal{E}\left(t_{(i)}\right)\) do not contain any positional information, one can typically add positional encodings, which is the map \(\mathcal{P}^{\star}: \mathbb{E}^{\star} \rightarrow \mathbb{E}^{\star}\). In the absolute position encoding setting, the commonly used form is the addition:
\[\begin{equation} \mathcal{P}^{\star}\left(\left\{\boldsymbol{e}_{(j)}\right\}_{j=1}^{r}\right):=\left\{\boldsymbol{e}_{(j)}+\boldsymbol{p}_{(j)}\right\}_{j=1}^{r} \end{equation}\]where \(p: \mathbb{N} \rightarrow \mathbb{E}\) is an injective function. In the learned variant of absolute position encoding, \(\boldsymbol{p}_{(j)}\) is learned during training. In the sinusoidal variant, denote \(\left(\boldsymbol{p}_{(j)}\right)\) as the $s$-th component of the vector, then \(\boldsymbol{p}_{(j)}\) is commonly computed as:
\[\begin{equation} \left(\boldsymbol{p}_{(j)}\right)_{s}= \begin{cases}\sin \left(\frac{j}{M^{\frac{s}{d}}}\right) \quad s=2 k \\ \cos \left(\frac{j}{M^{\frac{s-1}{d}}}\right) \quad s=2 k-1\end{cases} \end{equation}\]where \(s \in [0,d-2]\), and \(M=10^4\) are fixed
So far, the text \(\left\{a_{(i)}\right\}_{i=1}^{p}\in \mathbb{A}^{\star}\) has been transformed into a sequence of embeddings through three steps: tokenization \(\mathcal{K}\), embedding \(\mathcal{E}\), and positional encoding \(\mathcal{P}\) :
\[\begin{equation} \boldsymbol{x}:=\left(\mathcal{P}^{\star} \circ \mathcal{E}^{\star} \circ \mathcal{K}^{\star}\right)\left(\left\{a_{(i)}\right\}_{i=1}^{p}\right)=\left\{\boldsymbol{e}_{(j)}+\boldsymbol{p}_{(j)}\right\}_{j=1}^{r} \end{equation}\]where \(\boldsymbol{x} \in \mathbb{E}^{\star}\), and the length of which depends on both the tokenization algorithm and the choice of text.
Transformer \(\mathcal{T}\). The transformer can be represented as a neural network \(\mathcal{T}^{\star}: \mathbb{E}^{\star} \rightarrow \mathbb{E}^{\star}\), which maps a sequence of embeddings \(\left\{\boldsymbol{x}_{(t)}\right\}_{t=1}^{n}\) to another equal-length sequence, preserving the contextual information. For autoregressive tasks, the model is designed to ensure that each element of its output, e.g. $i$-th element of \(\mathcal{T}\left(\left\{\boldsymbol{x}_{(t)}\right\}_{t>i=1}^{n}\right)\), depends only on the previous embedded tokens \(\left\{\boldsymbol{x}_{(t)}\right\}_{t=1}^{t \leq i}\) and is independent of \(\left\{\boldsymbol{x}_{(t)}\right\}_{t=1}^{t \geq 1}\), which creates the masked structure that produces one-way information flow.
The transformer is typically defined by a composition of \(L \in \mathbb{N}\) residual blocks, consisting of self-attention mapping \(\mathcal{A}^{(l)}\), entrywise applied normalizing layers \(\mathcal{N}_{\mathcal{A}}^{(l)}, \mathcal{N}_{\mathcal{M}}^{(l)}\), and multiplayer perceptrons (MLP) layer \(\mathcal{M}^{(l)}\) :
\[\begin{equation} \displaylines{ \mathcal{T}^{\star}:=\left[\left(I+\mathcal{M}^{(l) \star} \circ \mathcal{N}_{\mathcal{M}}^{(l) \star}\right) \circ\left(I+\mathcal{A}^{(l)} \circ \mathcal{N}_{\mathcal{A}}^{(l) \star}\right)\right] \circ \dots \\ \circ\left[\left(I+\mathcal{M}^{(2) \star} \circ \mathcal{N}_{\mathcal{M}}^{(2) \star}\right) \circ\left(I+\mathcal{A}^{(2)} \circ \mathcal{N}_{\mathcal{A}}^{(2) \star}\right)\right] \circ\left[\left(I+\mathcal{M}^{(1) \star} \circ \mathcal{N}_{\mathcal{M}}^{(1) \star}\right) \circ\left(I+\mathcal{A}^{(1)} \circ \mathcal{N}_{\mathcal{A}}^{(1) \star}\right)\right] } \label{eq:5.6} \end{equation}\]where \(I\) denotes the identity mapping, inspired by residual neural networks (ResNet)
Transformer: Layer Normalization \(\mathcal{N}\). The normalizing layer can be interpreted as a re-parametrization with a learnable mean and standard deviation to stabilize training. In its original formulation
Recently works
and thus, combine the result of Equation \eqref{eq:5.7} and Equation \eqref{eq:5.8} , we can reformulate layer normalization \(\mathcal{N}\) as :
\[\begin{equation} \displaylines{ & \mathcal{N}(\boldsymbol{x})=\frac{\gamma(\boldsymbol{x}-\boldsymbol{\mu})}{\boldsymbol{\sigma}}+\beta=\gamma \cdot \frac{\boldsymbol{x}-\boldsymbol{\mu}}{\sqrt{\frac{1}{d}} \sqrt{\sum_{i=1}^{d}\left(x_{i}-\mu\right)^{2}}}+\beta \\ & =\gamma \cdot \frac{\boldsymbol{x}-\boldsymbol{\mu}}{\left(\frac{1}{\sqrt{d}}\right)\|\boldsymbol{x}-\boldsymbol{\mu}\|_{2}}+\beta=\gamma \cdot \frac{\sqrt{d} \cdot \operatorname{proj}_{\mathcal{H}}(\boldsymbol{x})}{\left\|\operatorname{proj}_{\mathcal{H}}(\boldsymbol{x})\right\|_{2}}+\beta } \label{eq:5.9} \end{equation}\]where \(\gamma, \beta \in \mathbb{E}\) are defined as the gain and bias learnable parameters. From a geometric viewpoint, layer normalization \(\mathcal{N}\) projects \(\boldsymbol{x} \in \mathbb{E}\) onto the hyperplane \(\mathcal{H}\) perpendicular to \(\overrightarrow{\mathbf{1}}\), and normalizes the projection such that it lies on the surface of the hyper-sphere \(\mathbb{S}^{d-1}\) of radius \(\sqrt{d}\). Also, considering the property of transformer-based architectures, all intermediate layers project onto the same hyper-sphere \(\mathbb{S}^{d-1}\). The parameter \(\gamma\) scales each coordinate axis of \(\mathbb{E}\) independently, transforming the hyper-sphere \(\mathbb{S}^{d-1}\) into a hyper-ellipsoid, and the bias term \(\beta\) shifts the center of the hyper-ellipsoid from the origin.
Moreover, according to the latest work
Transformer: Multilayer Percpetrons \(\mathcal{M}\). The MLP layer is a standard feed-forward neural network consisting of compositions of affine mappings \({ }_{m}^{n} \mathcal{L}^{(l)}: \mathbb{R}^{m} \rightarrow \mathbb{R}^{n}\) and Lipschitz functions \(\sigma(\cdot): \mathbb{R} \rightarrow \mathbb{R}\). We first define the affine mapping \({ }_{m}^{n} \mathcal{L}^{(l)}(t):=\boldsymbol{W}^{(l)} t+b^{(l)}\), where the weight matrix \(\boldsymbol{W}^{(l)} \in \mathbb{R}^{n \times m}\) and the bias vector \(b^{(l)} \in \mathbb{R}^{n}\). A typical MLP \(\mathcal{M}: \mathbb{E} \rightarrow \mathbb{E}\) used in transformers is then:
\[\begin{equation} \mathcal{M}:={ }_{d^{\prime}}^{d} \mathcal{L}^{(l)} \circ \sigma \circ{ }_{d}^{d^{\prime}} \mathcal{L}^{(l)} \end{equation}\]where $d^{\prime} \in \mathbb{N}$, usually $d^{\prime}>d$, and $l$ here indicates layer number. Typically, one considers ReLU, GELU, or sigmoid for the choice of activation function \(\sigma\)
Transformer: Self-attention \(\mathcal{A}\). As shown in Equation \eqref{eq:5.6}, the self-attention layer \(\mathcal{A}: \mathbb{E}^{\star} \rightarrow \mathbb{E}^{\star}\) is the only layer that combines embeddings of different tokens, which means \(\mathcal{A}\) attends to other tokens. Recall that we use \(\left\{\boldsymbol{x}_{(j)}\right\}_{j=1}^{n}\) to denote the given input sequence of length $n$, then the self-attention mechanism is defined as follows:
\[\begin{equation} \mathcal{A}\left(\boldsymbol{X}, \boldsymbol{W}_{Q}, \boldsymbol{W}_{K}, \boldsymbol{W}_{V}\right):=\operatorname{softmax}\left(\frac{\boldsymbol{Q} \boldsymbol{K}^{T}}{\sqrt{d}}\right) \boldsymbol{V} \label{eq:5.11} \end{equation}\]where \(\boldsymbol{X}=\left\{\boldsymbol{x}_{(j)}\right\}_{j=1}^{n} \in \mathbb{R}^{d \times n}\) for conciseness, and
\[\begin{equation} \boldsymbol{Q}:=\boldsymbol{X}^{T} \boldsymbol{W}_{Q} \quad \boldsymbol{K}:=\boldsymbol{X}^{T} \boldsymbol{W}_{K} \quad \boldsymbol{V}:=\boldsymbol{X}^{T} \boldsymbol{W}_{V} \label{eq:5.12} \end{equation}\]To normalize the probabilities, we here introduce the softmax function softmax : $\mathbb{R}^{\star} \rightarrow[0,1]^{\star}$ denoted as:
\[\begin{equation} \operatorname{softmax}\left(\boldsymbol{x}_{(i)}\right):=\frac{\exp \left(\boldsymbol{x}_{(i)}\right)}{\sum_{j=1}^{n} \exp \left(\boldsymbol{x}_{(j)}\right)} \label{eq:5.13} \end{equation}\]Here, \(\boldsymbol{W}_{Q}, \boldsymbol{W}_{K} \in \mathbb{R}^{d \times k}\) and \(\boldsymbol{W}_{V} \in \mathbb{R}^{d \times v}\) are projection matrices from \(\mathbb{R}^{d}\) to an intermediate dimension \(\mathbb{R}^{k}\) and value dimension \(\mathbb{R}^{v}\). Notices that for the settings of multi-head attention, the projection matrices can be written as \(\boldsymbol{W}_{Q}^{(i)}, \boldsymbol{W}_{K}^{(i)}, \boldsymbol{W}_{V}^{(i)}\), where \(i \in[1, \ldots, h]\) and $h$ is the number of heads. According to the original design of transformers
where \(\boldsymbol{W}_{O}^{(i)} \in \mathbb{R}^{k \times d}\) denotes an element of the partition of matrix \(\boldsymbol{W}_{O} \in \mathbb{R}^{h k \times d}\) alongside the row dimension. By combining the Equation \eqref{eq:5.11} to Equation \eqref{eq:5.14} , we can derive a simple form notation:
\[\begin{equation} \displaylines{ \operatorname{MultiHead}(\boldsymbol{X})=\sum_{i=1}^{h} \operatorname{softmax}\left(\frac{\boldsymbol{X}^{T} \boldsymbol{W}_{Q}^{(i)} \boldsymbol{W}_{K}^{(i) T} \boldsymbol{X}}{\sqrt{d}}\right) \boldsymbol{X}^{T} \boldsymbol{W}_{V}^{(i)} \boldsymbol{W}_{O}^{(i)} \\ =\sum_{i=1}^{h} \operatorname{softmax}\left(\frac{\boldsymbol{X}^{T} \boldsymbol{W}_{Q K}^{(i)} \boldsymbol{X}}{\sqrt{d}}\right) \boldsymbol{X}^{T} \boldsymbol{W}_{V O}^{(i)} } \label{eq:5.15} \end{equation}\]where \(\boldsymbol{W}_{Q K}^{(i)}=\boldsymbol{W}_{Q}^{(i)} \boldsymbol{W}_{K}^{(i) T}, \boldsymbol{W}_{V O}^{(i)}=\boldsymbol{V}_{Q}^{(i)} \boldsymbol{W}_{O}^{(i)}\), and \(\boldsymbol{W}_{Q K}^{(i)}, \boldsymbol{W}_{V O}^{(i)} \in \mathbb{R}^{d \times d}\) are both low-rank virtual matrices as previous works shown
On a high level, the term $\left(\frac{Q K^{T}}{\sqrt{d}}\right)$ can be interpreted as measuring the similarities between the embeddings of the $i$-th query and the $j$-th key across all tokens. Consequently, softmax mapping softmax $\left(\frac{Q K^{T}}{\sqrt{d}}\right)$ can be understood as representing the probabilities distribution that the $i$-th query will attend to or focus on the $j$-th key.
The scaling factor $\frac{1}{\sqrt{d}}$ is introduced to mitigate the effect of large magnitudes in the dot products, which can cause the softmax function to generate extreme probabilities when $d$ is high. By scaling the dot products by $\frac{1}{\sqrt{d}}$, the self-attention mechanism becomes more stable and less sensitive to the embedding dimensionality.
In summary, the self-attention mechanism allows the model to dynamically focus on different parts of the input sequence, emphasizing the most relevant information for predicting subsequent elements.
Prediction Head \(\mathcal{H}\). The prediction head or un-embedding layer can be represented as the mapping \(\mathcal{H}: \mathbb{E}^{\star} \rightarrow \Delta^{\gamma}\), where
\[\begin{equation} \Delta^{\gamma}:=\left\{\boldsymbol{u} \in[0,1]^{\gamma} \mid \sum_{i=1}^{\gamma}\left\|\boldsymbol{u}_{i}\right\|=1\right\} \label{eq:5.16} \end{equation}\]denotes the probability simplex in \(\mathbb{R}^{\gamma}\), which is a geometric representation of all possible distributions of probabilities across $\gamma$ different outputs. The prediction head maps the sequence of transformed embeddings \(\boldsymbol{Y}:=\mathcal{T}(\boldsymbol{X})\) to a vector \(\boldsymbol{u} \in \Delta^{\gamma}\), where \(\boldsymbol{u}_{i}\) denotes the probability of predicting the next token \(t_{(q+1)} \in \mathbb{T}\). As the transformed embedding of the last tokens, e.g. \(\boldsymbol{y}_{n+1}\), contains information about the entire input sequence \(\left\{\boldsymbol{x}_{(t)}\right\}_{i=1}^{n}\), a straightforward approach is to use a linear mapping followed by softmax layer to ensure \(\boldsymbol{u}\) lies inside \(\Delta^{\gamma}\) :
\[\begin{equation} \boldsymbol{u}:=\left(\operatorname{softmax} \circ_{d}^{\gamma} \mathcal{L}\right)\left(\boldsymbol{y}_{(n+1)}\right) \label{5.17} \end{equation}\]Sampling $\mathcal{S}$. Sampling methods $\mathcal{S}: \Delta^{\gamma} \rightarrow \mathbb{T}$ are the decoding strategies for language models to generate coherent, diverse, and contextually relevant texts, which determine how the final prediction for the next token $t_{(q+1)} \in \mathbb{T}$ is selected by sampling from the probability distribution over all possible tokens. Choosing the appropriate sampling method helps to decrease the occurrence of text degeneration, which implies the production of repetitive, incoherent, or generic texts
Several methods are commonly used in text generation, including beam search, top- $k$ sampling, and nucleus sampling
To sum up, the aforementioned operations can be iteratively applied to the augmented token sequence \(\left\{t_{(i)}\right\}_{i=1}^{q+1}\) repeatedly, thereby generating successive token \(t_{(q+2)}\) until the stopping criterion is finally satisfied:
\[\begin{equation} t_{(q+2)}:=\left(\mathcal{S} \circ \mathcal{H} \circ \mathcal{T}^{\star} \circ \mathcal{P}^{\star} \circ \mathcal{E}^{\star}\right)\left(\left\{t_{(i)}\right\}_{i=1}^{q+1}\right) \end{equation}\]In summary, tokens are first embedded as particles in $\mathbb{R}^{d}$ and then projected onto the hypersphere $\mathbb{S}^{d-1}$, travelling around its surface, thus completing a “walk of sentences” in response to the initial input of LLMs. The trajectory of the particle flow is determined by each layer of the transformer, which continually transforms “meanings” of particles. Meanwhile, the cumulative residual stream encodes information that has been progressively accumulated and transformed throughout the various blocks of the transformer’s architecture as the “communication channels”
5.2 Concepts Representation within LLMs
LLMs demonstrate a remarkable ability to answer questions and understand the underlying semantic intentions, which then raises questions about how knowledge are stored inside LLMs. Can we draw parallels between the memory circuits of the human brain with LLMs? Or, do LLMs mimic the functionality of biological neurons to store information?
Linear Concept Representation. We propose a mathematical language to formalize the inner workings of semantical knowledge storage of LLMs. Continuing along the perspective of Equation \eqref{eq:5.2}, we further investigate the hypothesis that linguistic concepts are represented in the internal vector space within LLMs.
Let $\mathbb{V}=\mathbb{R}^{d}$ denote the vector space that concepts are embedded into. We define the set of output words from LLMs as $\mathbb{W}=\left{w_{1}, w_{2}, \ldots, w_{n}\right}$, where each $w_{i}$ is a word from the dictionary $\mathbb{W}$. We denote the extended version of embedding mapping $\tilde{\mathcal{E}}: \mathbb{V} \rightarrow \mathbb{W}$ and un-embedding mapping $\tilde{\mathcal{E}}^{-1}: \mathbb{W} \rightarrow \mathbb{V}$ as follows:
\[\begin{equation} \displaylines{ & \tilde{\mathcal{E}}\left(w_{i}\right):=(\mathcal{T} \circ \mathcal{P} \circ \mathcal{E} \circ \mathcal{K})\left(w_{i}\right) \\ & \tilde{\mathcal{E}}^{-1}\left(\tilde{\mathcal{E}}\left(w_{i}\right)\right):=(\mathcal{S} \circ \mathcal{H})\left(\tilde{\mathcal{E}}\left(w_{i}\right)\right) } \label{5.20} \end{equation}\]and it is trivial to show that:
\[\begin{equation} \displaylines{ \tilde{\mathcal{E}}\left(\text { ' word' }\right)=\left(\mathcal{T}^{\star} \circ \mathcal{P}^{\star} \circ \mathcal{E}^{\star} \circ \mathcal{K}^{\star}\right)(\text { 'word' }) \in \mathbb{V} \\ \left(\tilde{\mathcal{E}}^{-1} \circ \tilde{\mathcal{E}}\right)(\text { 'word' })=\text { 'word' }^{\mathbb{W}} } \end{equation}\]For simplicity, we restrict focus on binary concepts, which are the vectors composed of their corresponding counterfactual parts. We denote the counterfactual parts as \(\delta_{+}\) or \(\delta_{-}\), where e.g. \(\delta_{+} \in \text\{ 'man', 'king', 'actor', \ldots \} \subset \mathbb{W}\) and \(\delta_{-} \in\text\{ 'woman', 'queen', 'actress', \ldots\} \subset \mathbb{W}\). The positive span
We then say binary concept vectors \(\vec{b}_{i}, \vec{b}_{j} \in \mathbb{V}\) are linearly separable if and only if their counterfactual parts \(\delta_{+}^{(i)}, \delta_{-}^{(i)}, \delta_{+}^{(j)}, \delta_{-}^{(j)}\) belong to the same separable category. The binary concept vector \(\vec{b}_{i}\) is then defined as the difference between the extended embeddings of its counterfactual parts:
\[\begin{equation} \tilde{\mathcal{E}}\left(\delta_{+}^{(i)}\right)-\tilde{\mathcal{E}}\left(\delta_{-}^{(i)}\right) \in \operatorname{span}^{+}\left(\vec{b}_{i}\right) \label{eq:5.23} \end{equation}\]Thus Equation \eqref{eq:5.2} can be re-interpreted as the expression of linearly separable binary concept (here means “gender”):
\[\begin{equation} \tilde{\mathcal{E}}\left(\delta_{+}^{\text {(gender) }}\right)-\tilde{\mathcal{E}}\left(\delta_{-}^{(\text {gender) }}\right) \in \operatorname{span}^{+}\left(\vec{b}_{(\text {gender })}\right) \label{eq:5.24} \end{equation}\]Linearity. As we have shown in Equation \eqref{eq:5.16} and Equation \eqref{eq:5.17}, LLMs produce the probability distribution over different outputs, which is proportional to the softmax of attention scores. LLMs digest context text \(w_j\), then sample the output text \(w_i\) by the mechanism of softmax:
\[\begin{equation} \displaylines{ P\left(w_{i} \mid w_{j}\right) & :=\operatorname{softmax}\left(\left\langle\tilde{\mathcal{E}}\left(w_{j}\right), \tilde{\mathcal{E}}\left(w_{i}\right)\right\rangle\right) \\ & =\frac{e^{\left\langle\tilde{\varepsilon}\left(w_{j}\right), \tilde{\mathcal{E}}\left(w_{i}\right)\right\rangle}}{\sum\limits_{k=1}^{|\mathbb{W}|} e^{\left\langle\tilde{\mathcal{E}}\left(w_{j}\right), \tilde{\mathcal{\varepsilon}}\left(w_{k}\right)\right\rangle}} } \label{eq:5.25} \end{equation}\]Before we draw the conclusion of linearity, we first need to define an inner product on \(\mathbb{V}\) to measure the similarity or projection between vectors in the representation space. Let \(\boldsymbol{B} \in \mathbb{R}^{d \times d}\) be a symmetric positive definite matrix, and define the inner product \(\langle\cdot, \cdot\rangle_{B}: \mathbb{V} \times \mathbb{V} \rightarrow \mathbb{R}\) as follows:
Notices that the inner product, induced by matrix \(\boldsymbol{B}\), should satisfy the following properties for \(\vec{b}_{i}, \vec{b}_{j} \in \mathbb{V}, \alpha \in \mathbb{R}\):
\[\begin{equation} \left\{\begin{array}{l} \left\langle\vec{b}_{i}, \vec{b}_{j}\right\rangle_{B}=\left\langle\vec{b}_{j}, \vec{b}_{i}\right\rangle_{B} \tag{5.26}\\ \left\langle\alpha \vec{b}_{i}, \vec{b}_{j}\right\rangle_{B}=\alpha\left\langle\vec{b}_{i}, \vec{b}_{j}\right\rangle_{B} \\ \left\langle\vec{b}_{i}+\vec{b}_{k}, \vec{b}_{j}\right\rangle_{B}=\left\langle\vec{b}_{i}, \vec{b}_{j}\right\rangle_{B}+\left\langle\vec{b}_{k}, \vec{b}_{j}\right\rangle_{B} \\ \left\langle\vec{b}_{j}, \vec{b}_{j}\right\rangle_{B}>0, \text { for all } \vec{b}_{j} \in \mathbb{V} \backslash\{0\} \end{array}\right. \label{eq:5.26} \end{equation}\]As we have the notion of inner product, considering \(w_{i} \in\left\{\delta_{+}^{(k)}, \delta_{-}^{(k)}\right\}$, e.g. $w_{i}=\delta_{+}^{(k)}\), then \(w_{i}\) implies the existence of binary vector \(\vec{b}_{k}\), which shares a logit-linear probability of occurrence:
\[\begin{equation} \displaylines{ \operatorname{logit}\left[P\left(\delta_{+}^{(k)} \mid w_{j}\right)\right]=\ln \left[\frac{P\left(\delta_{+}^{(k)} \mid w_{j}\right)}{1-P\left(\delta_{+}^{(k)} \mid w_{j}\right)}\right]=\ln \left[\frac{e^{\left\langle\tilde{\mathcal{E}}\left(w_{j}\right), \tilde{\mathcal{E}}\left(\delta_{+}^{(k)}\right)\right\rangle_{B}}}{e^{\left\langle\tilde{\mathcal{E}}\left(w_{j}\right), \tilde{\mathcal{E}}\left(\delta_{-}^{(k)}\right)\right\rangle_{B}}}\right] \\ =\tilde{\mathcal{E}}\left(w_{j}\right)^{T} \boldsymbol{B} \tilde{\mathcal{E}}\left(\delta_{+}^{(k)}\right)-\tilde{\mathcal{E}}\left(w_{j}\right)^{T} \boldsymbol{B} \tilde{\mathcal{E}}\left(\delta_{-}^{(k)}\right) \\ =\tilde{\mathcal{E}}\left(w_{j}\right)^{T} \boldsymbol{B}\left(\tilde{\mathcal{E}}\left(\delta_{+}^{(k)}\right)-\tilde{\mathcal{E}}\left(\delta_{-}^{(k)}\right)\right)=\left(\lambda \tilde{\mathcal{E}}\left(w_{j}\right)^{T} \boldsymbol{B}\right) \overrightarrow{b_{k}} } \label{eq:5.27} \end{equation}\]where \(\lambda \in \mathbb{R}\), and \(\tilde{\mathcal{E}}\left(w_{j}\right)^{T} \boldsymbol{B}\) is a coefficient item. Then the probability of the output is logitlinear in the language model subspace representation.
Limitations of Linearity. While the linearized representation allows LLMs to exploit linear relationships between linguistic concepts and uncover underlying semantic structures, it is essential to acknowledge the limitations of the linearity hypothesis. Considering the complexity essence of language, to further explore these nonlinear aspects, we propose viewing the semantic space as a manifold \(\mathcal{W}\) equipped with a Riemannian metric \(\boldsymbol{g}\). We believe this perspective will open up new ideas for investigating the geometric properties of language.
-
The inner product of vectors, defined as \(\left\langle\tilde{\mathcal{E}}\left(w_{i}\right), \tilde{\mathcal{E}}\left(w_{j}\right)\right\rangle\), can represent the semantic similarity between two words \(w_{i}\) and \(w_{j}\).
-
The outer product of vectors, given by \(\tilde{\mathcal{E}}\left(w_{i}\right) \otimes \tilde{\mathcal{E}}\left(w_{j}\right)\), can capture the combination of the semantics of two words, which is a potential “meaning-blending” mechanism.
-
Linear combinations of vectors, such as \(t \tilde{\mathcal{E}}\left(w_{i}\right)+(1-t) \tilde{\mathcal{E}}\left(w_{j}\right)\) where \(t \in[0,1]\), can represent the interpolation of word meanings or even “semantic gradients”.
-
Linear transformations applied to vectors, denoted as \(\boldsymbol{A} \tilde{\mathcal{E}}\left(w_{i}\right)\) where \(\boldsymbol{A}\) is denotes the linear transformation matrix, can model the “semantic rotation” or “dimensionality projection”, potentially inspiring applications in sentiment analysis and related fields.
-
Geodesics, which are the shortest paths between points on the manifold \(\mathcal{W}\), can be employed to explore the continuity and smoothness of language. These geodesics reflect the properties of a word’s local neighborhood on its tangent space, providing insights into the local structure of the semantic space.
In short, the framework of internal representation of information demonstrates the model’s capability to accurately comprehend complex semantic information. And the vector space modeling of linguistic concepts within LLMs underpins their ability to capture and process the semantic information present in human language.
5.3 Integration with Localized Knowledge Bases
The integration of localized knowledge bases with LLMs is formalized through the retrieval-augmented generation framework, and is crucial for enhancing their interpretability. This approach significantly enhances the model’s capability to produce accurate and contextually relevant outputs.
Detailed mathematical modeling of the retrieval processes used in RAG, which involve nearest neighbor searches in a high-dimensional vector space, showcases how external knowledge is incorporated into the generation process. The retrieval mechanism in a RAG framework can be described mathematically as follows:
Vector Representation and Embedding:
Each text or data point \(\mathcal{D}\) in the knowledge base is transformed into a vector space using an embedding model \(\tilde{\mathcal{E}}(\mathcal{D})\), which maps the semantic content of documents into a high-dimensional vector space \(\mathbb{R}^{d}\).
\[\begin{equation} \boldsymbol{v}=\tilde{\mathcal{E}}(\mathcal{D}) \end{equation}\]Query Processing:
A query \(\mathcal{Q}\) from users is similarly embedded into the same vector space.
\[\begin{equation} \boldsymbol{q}=\tilde{\mathcal{E}}(Q) \end{equation}\]Similarity Calculation:
The relevance of each document to the query is computed using a similarity metric, typically the cosine similarity, between the query vector and document vectors.
\[\begin{equation} \operatorname{similarity}(\boldsymbol{q}, \boldsymbol{v}):=\frac{\boldsymbol{q} \cdot \boldsymbol{v}}{\|\boldsymbol{q}\|\|\boldsymbol{v}\|} \end{equation}\]Retrieval:
The retrieval function can be formulated as a nearest neighbor search problem in the vector space, which selects the document vector that has the highest similarity score with the query vector, thus deciding which external knowledge is most relevant to the current context.
\[\begin{equation} \operatorname{retrieve}(Q):=\underset{D \in \mathcal{D}}{\arg \max } \operatorname{similarity}(\tilde{\mathcal{E}}(\mathcal{Q}), \tilde{\mathcal{E}}(D)) \end{equation}\]Integration of External Knowledge:
Once the relevant documents are retrieved, their content is seamlessly integrated into the generative process of the language model. This integration augments the generative model’s capability to produce more accurate and contextually rich responses. The integration can be mathematically modeled as a function that combines the retrieved information into the generation process.
In summary, in Chapter 5 we propose that:
-
Tokens in LLMs are represented as “particles” embedded in a \(\mathbb{R}^{d}\) space and subsequently projected onto a hyper-sphere \(\mathbb{S}^{d-1}\), simulating a “walk of sentences” on its surface in response to input stimuli.
-
These particles follow trajectories shaped by the transformer layers, which modify the “meanings” of the particles through each transformation stage.
- Layers of transformers act as “flow maps” in the probability space $\mathcal{P}(\mathbb{R}^{d})$
The space $\mathcal{P}(\mathbb{R}^{d})$ represents all possible ways to distribute a set of probabilities over $\mathbb{E}=\mathbb{R}^{d}$. , directing the trajectory of these probability particles, which enhances our understanding of how the model generates language and processes semantic information. - By integrating external, domain-specific knowledge, the model’s decisions become more interpretable, shedding light on the complex systems within LLMs. This framework not only facilitates a deeper understanding of the internal mechanisms of LLMs but also improves their transparency and efficacy in real-world applications.
6. Experimental Results
The process of constructing the domain-specific knowledge base has yielded substantial insights. In this section, we will explore the intriguing observations that emerged from this practice. These findings are presented as examples of how to merge RAG frameworks with open-source language models that are applied in real-world settings.
6.1 The Dynamics of Transformers
Motivated by recent studies
ResNet Dynamics. Among the class of neural networks, ResNets have become a prominent architecture since their introduction in
where \(\Theta=(w(\cdot), b(\cdot))\) are trainable parameters. We define the hidden layer number here $l$, and we can naturally interpret layer index as a time variable, for \(t \in(0, T)\) :
\[\begin{equation} \displaylines{ \left\{\begin{array}{l} \boldsymbol{x}(0)=x \\ \dot{\boldsymbol{x}}(t)=\sigma\left(w_{(k)} \boldsymbol{x}(t)+b_{(k)}\right) \end{array}\right. } \end{equation}\]Simplified Transformer Dynamics Model. Unlike ResNets, transformers operate on a sequence of vectors of length $n$, namely \(\left\{\boldsymbol{x}_{(j)}(0)\right\}_{j=1}^{n} \in\left(\mathbb{R}^{d}\right)^{n}\), where each element of sequence \(\boldsymbol{x}_{(j)}(0) \in \mathbb{R}^{d}\) is a token and the entire sequence a prompt. Recall our mathematical derivation on LLMs in Section 5.1, we rewrite the self-attention matrix \(\boldsymbol{A}_{i j}\) in self-attention \(\mathcal{A}\) as:
\[\begin{equation} \boldsymbol{A}_{i j}:=\operatorname{softmax}\left(\frac{\boldsymbol{Q} \boldsymbol{K}^{T}}{\sqrt{d}}\right)=\frac{e^{\beta\left\langle\boldsymbol{x}_{(i)}^{T}(t) \boldsymbol{W}_{Q(t)}, \boldsymbol{x}_{(j)}^{T}(t) \boldsymbol{W}_{K(t)}\right\rangle}}{\sum_{j=1}^{n} e^{\beta\left\langle\boldsymbol{x}_{(i)}^{T}(t) \boldsymbol{W}_{Q(t)}, \boldsymbol{x}_{(j)}^{T}(t) \boldsymbol{W}_{K(t)}\right\rangle}} \label{eq:6.3} \end{equation}\]With the perspective of nonlinear coupling mechanism in the interacting particle system, the self-attention matrix \(\boldsymbol{A}_{i j} \in \mathbb{R}^{n \times n}\) captures the attention given by particle $i$ to particle $j$ relatively to all particles \((i, j \in[0, n])\). Numerical observations
As the result of Equation \eqref{eq:5.9}, layer normalization effectively constrains particles to a timevarying hyper-ellipsoid defined by the \(\sqrt{d}\) radius hyper-sphere \(\mathbb{S}^{d-1}\). We can further assume the existence of a smooth isomorphism that projects the points on the hyper-sphere \(\mathbb{S}^{d-1}\) to the unit sphere \(\tilde{\mathbb{S}}^{d-1}\). Under such setting, a transformer can be interpreted as a flow map on the space \(\left(\tilde{\mathbb{S}}^{d-1}\right)^{n}\), in which the input embedding vectors \(\left\{\boldsymbol{x}_{(j)}(0)\right\}_{j=1}^{n} \in \mathbb{R}^{d \times n}\) can be viewed as the initial condition. Then we have attention layer \(\mathcal{A}\) as follows:
\[\begin{equation} \mathcal{A}\left(\left\{\boldsymbol{x}_{(j)}(0)\right\}_{j=1}^{n}\right)=\boldsymbol{A}_{i j} \boldsymbol{x}_{(j)}^{T}(t) \boldsymbol{W}_{V}=\frac{e^{\beta\left\langle\boldsymbol{x}_{(i)}^{T}(t) \boldsymbol{W}_{Q(t)}, \boldsymbol{x}_{(j)}^{T}(t) \boldsymbol{W}_{K(t)}\right\rangle} \boldsymbol{x}_{(j)}^{T}(t) \boldsymbol{W}_{V(t)}}{\sum_{j=1}^{n} e^{\beta\left\langle\boldsymbol{x}_{(i)}^{T}(t) \boldsymbol{W}_{Q(t)}, \boldsymbol{x}_{(j)}^{T}(t) \boldsymbol{W}_{K(t)}\right\rangle}} \label{eq:6.4} \end{equation}\]To illustrate our conclusions in a simplified scenario wherein the trainable parameters matrices \(\boldsymbol{W}_{Q(t)}, \boldsymbol{W}_{K(t)}, \boldsymbol{W}_{V(t)}\) are all equal to the identity unless stated otherwise, we can derive the single-head transformer dynamics (without MLP) as follows:
\[\begin{equation} \boldsymbol{x}_{(j)}(t)=\operatorname{proj}_{T_{x} \tilde{\mathbb{S}}}\left(\frac{\sum_{j=1}^{n} e^{\beta\left\langle\boldsymbol{x}_{(i)}(t), \boldsymbol{x}_{(j)}(t)\right\rangle} \boldsymbol{x}_{(j)}(t)}{\sum_{k=1}^{n} e^{\beta\left\langle\boldsymbol{x}_{(i)}(t), \boldsymbol{x}_{(k)}(t)\right\rangle}}\right) \label{eq:6.5} \end{equation}\]where \(\operatorname{proj}_{T_{x}} \tilde{\mathbb{S}}\) denotes the projection from unit sphere \(\tilde{\mathbb{S}}\) to its tangent space \(T_{x} \tilde{\mathbb{S}}\). Recall that we considering the output of a transformer as the probability measure, thus capturing the likelihood of the next token, one can view the transformer as the flow map between probability measure on \(\tilde{\mathbb{S}}\).In summary, the dynamics within transformer-based LLMs present a complex yet intriguing study of the flow between probability measures on the unit sphere.
Inspired by previous mentioned theoretical frameworks, it is hypothesized that the final candidates for the next token can be viewed as a clustering of tokens within the “token space”, which can be interpreted as a small number of possible outcomes. To experimentally verify this, we model the dynamics of transformers under a less restrictive condition, simulating scenarios with different clustering phenomena.
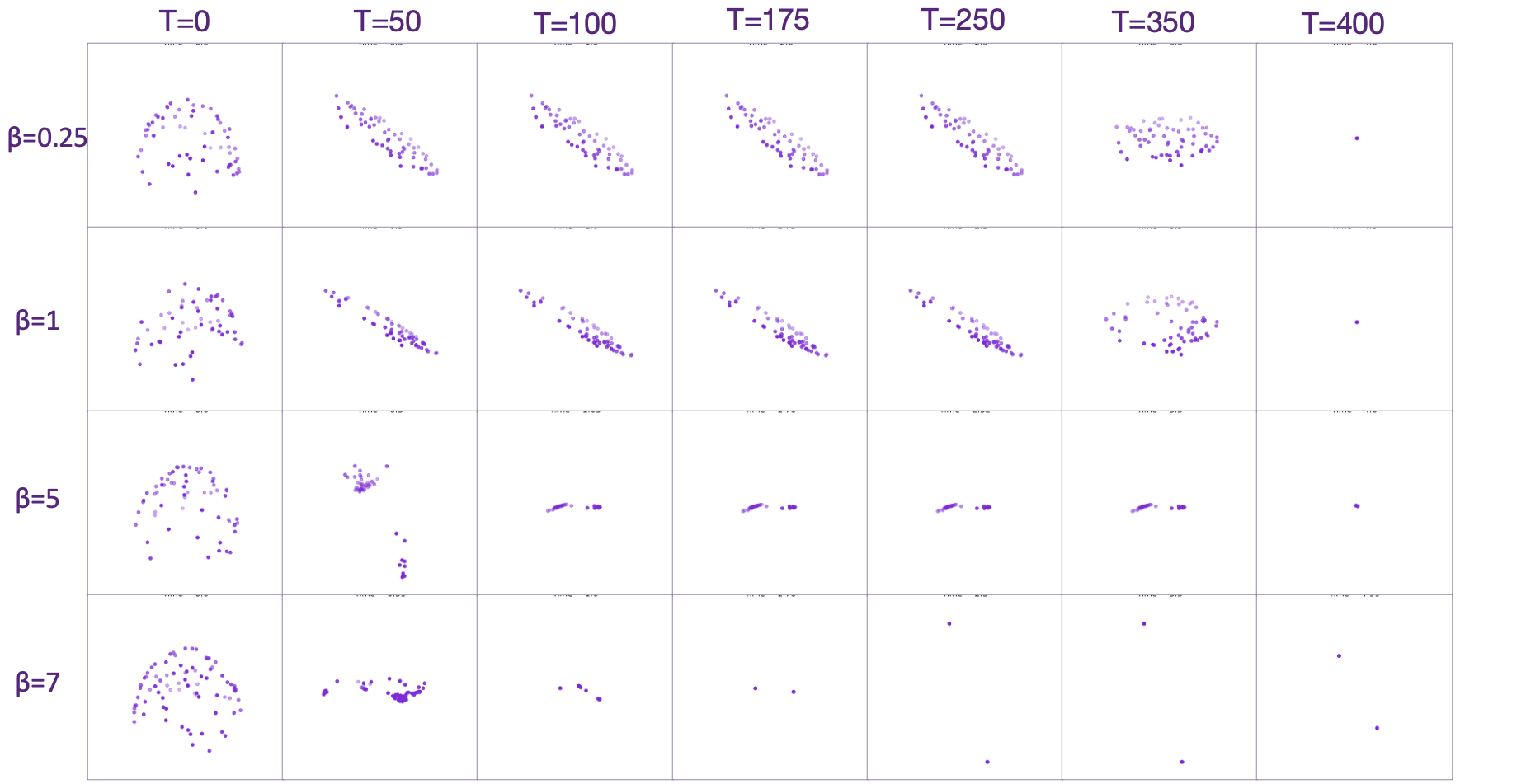
Axes3D from matplotlib to visualize the position-updating process of the input tokens inside a transformer system, which is determined by attention weights (moderated by $\beta$ ) and the positions of other points. The setup involves initializing random points on a three-dimensional sphere $\mathbb{S}^{3}$, with $n=60$ initial points, and observing cluster phenomena at varying $\beta$ values. Results indicate that adjusting $\beta$ controls the overall sensitivity and dynamic characteristics of the system. Faster clustering occurs at higher $\beta$ values, while slower clustering phenomena are observed at lower $\beta$ values. Originally, transformers update their internal states based on a sequence of operations involving layer normalization and softmax layers. By rescaling the vectors \(\left\{\boldsymbol{x}_{(j)}(t)\right\}_{j=1}^{n}\) into a more simplified form \(\left\{\boldsymbol{x}_{(j)}(t)\right\}_{j=1}^{n}\), thus in accordance with the effect of the attention mechanism. The simplified model for transformer dynamics is then given by:
\[\begin{equation} \boldsymbol{z}_{(k)}(t)=e^{-t \boldsymbol{W}_{V} \boldsymbol{x}_{(k)}(t)} \end{equation}\]thereby simplifying the analysis to a focus on the exponential interaction component controlled by \(\beta\), which modulates the sensitivity of the exponential function, enhancing or attenuating the influence based on the inner products of the state vectors. Notice that \(\boldsymbol{W}_{Q(t)}=\boldsymbol{W}_{K(t)}=\boldsymbol{W}_{V(t)}=\boldsymbol{I}\), henceforth we can derive the dynamics of (single head) transformer-based language model by
\[\begin{equation} \left\{\begin{array}{l} \boldsymbol{z}_{(k+1)}(t)=\boldsymbol{z}_{(k)}(t)+\Delta t \cdot \boldsymbol{A}_{i j} \cdot \boldsymbol{z}_{(k)}^{T}(t) \\ \boldsymbol{z}_{(k)}(0)=\boldsymbol{x}_{(i)}(0) \end{array}\right. \end{equation}\]And thus, under the simplified condition, the core dynamics of the transformer are given by :
\[\begin{equation} \mathcal{T}\left(\left\{\boldsymbol{z}_{(j)}(0)\right\}_{j=1}^{n}\right)=\boldsymbol{A}_{i j} \cdot \boldsymbol{z}_{(k)}^{T}(t)=\frac{e^{\beta\left\langle\boldsymbol{z}_{(k)}^{T}(t), \boldsymbol{z}_{(j)}^{T}(t)\right\rangle}}{\sum\limits_{j=1}^{n} e^{\beta\left\langle\boldsymbol{z}_{(k)}^{T}(t), \boldsymbol{z}_{(j)}^{T}(t)\right\rangle}}=\frac{e^{\beta \boldsymbol{z}_{(k)}(t) \cdot \boldsymbol{z}_{(j)}^{T}(t)} \boldsymbol{z}_{(j)}^{T}(t)}{\sum\limits_{j=1}^{n} e^{\left.\beta \boldsymbol{z}_{(k)}(t) \cdot \boldsymbol{z}_{(j)}^{T}\right)(t)}} \end{equation}\]where the initial condition remains the same, and the coefficient matrix \(\boldsymbol{A}_{i j}\) indicates the strength of the attraction of \(\boldsymbol{z}_{(k)}\) to \(\boldsymbol{z}_{(j)}\), and parameter \(\beta\) affecting the form of clutering, as Figure 6.1 implies.
Our experiments demonstrate that transformers manage token dynamics through a complex interplay of attention mechanisms modulated by \(\beta\), suggesting a profound connection between transformer dynamics and fluid dynamics. This refined perspective on transformer dynamics underpins future analysis, guiding more inspiring insights for the mechanistic interpretability of LLMs.
6.2 RAG-enhanced LLMs

To effectively incorporate these knowledge bases into LLMs, technologies like the RAG framework are employed and have significant success. With the help of LangChain-Chatchat, we can employ the RAG framework easily, which paves the way for the construction of question-answering digital avatars with localized knowledge bases. The retrieval component is generally a neural network trained to identify and fetch documents pertinent to the query at hand, while the generative component adapts this information into the response generated by the LLMs, thus significantly enhancing the accuracy and relevance of the model’s outputs.
6.3 Hyperparameter Tuning
In our experiments, we also ventured into the realm of hyperparameter tuning, adjusting variables including but not limited to the size of chunking windows, model temperature settings, and knowledge match rate settings. We observed that as the language model’s values approached zero, its alignment and acceptance of its own identity as a large language model were heightened; conversely, as values approached one, the model exhibited lower levels of skepticism about its role as an “artificial intelligence assistant” and its impersonal nature.
We found that maintaining the temperature value within a specific range ($0.2$ to $0.5$) and considering the context of historical dialogues influenced the knowledge match score threshold (related to the recall rate of data from the knowledge base). Our experiments commenced with a moderate threshold value of $0.5$, which we then adjusted based on the quality of the recalled data. For instance, if a threshold of $0.9$ yielded too little or no data, we would lower it to $0.1$ to determine whether more relevant data could be recalled. The knowledge match score threshold for LangChain-Chatchat showed optimal performance within the range of $0.6$ to $0.7$. These findings highlight the delicate balance required in setting hyperparameters to optimize both the precision and recall of relevant information, thereby enhancing the functionality and reliability of the language model in practical applications.
The main hyperparameters of the ChatGLM3-6B model are outlined as follows:
-
max_length: the total token limit for the model, encompassing both input and output tokens. -
temperature: this parameter adjusts the probability distribution of words. A lower temperature results in more deterministic outputs, while a higher temperature yields less certainty. -
top_p: a sampling strategy parameter of the model. At each step, the model samples randomly only from the smallest set of words whose cumulative probability exceeds a certain threshold $p$, disregarding other less probable words. This focuses on the core part of the probability distribution and ignores the tail.
For tasks targeting specific character portrayals in the digital avatar project, we aim for the intelligent agent to appear more human-like, less rigid, and sensitive, capable of producing creative and diverse textual outputs in alignment with the predefined character script. Simultaneously, it should provide accurate feedback based on information retrieved from the knowledge base, as demonstrated by the results in Figure 6.2.
Therefore, by fixing variables such as the content of the knowledge base, knowledge match score threshold, and historical input content, and by adjusting the temperature value, we experimentally determined an appropriate temperature range from $0.2$ to $0.4$ that avoids conflicts with the digital avatar’s identity and integrates seamlessly with the given identity in the prompt template. The experimental results are depicted below.


When the temperature $T$ is set very low (approaching $0.1$), the output from the LLM becomes highly deterministic and conforms closely to “conventional” responses, showing a strong alignment with its predefined “persona”. However, such outputs are often too monotonous and focused, lacking the flexibility required for LLMs operating with domain-specific knowledge bases, making it an unsuitable setting for the temperature parameter.
As $T$ values hover between $0.5$ and $0.6$, the outputs of the LLM exhibit uncertainty. This can be interpreted as the model having unstable self-recognition; sometimes it acknowledges its digital avatar persona, while at other times, it positions itself as purely an emotionless artificial intelligence model. This results in unpredictable personality traits and inconsistencies in its responses.
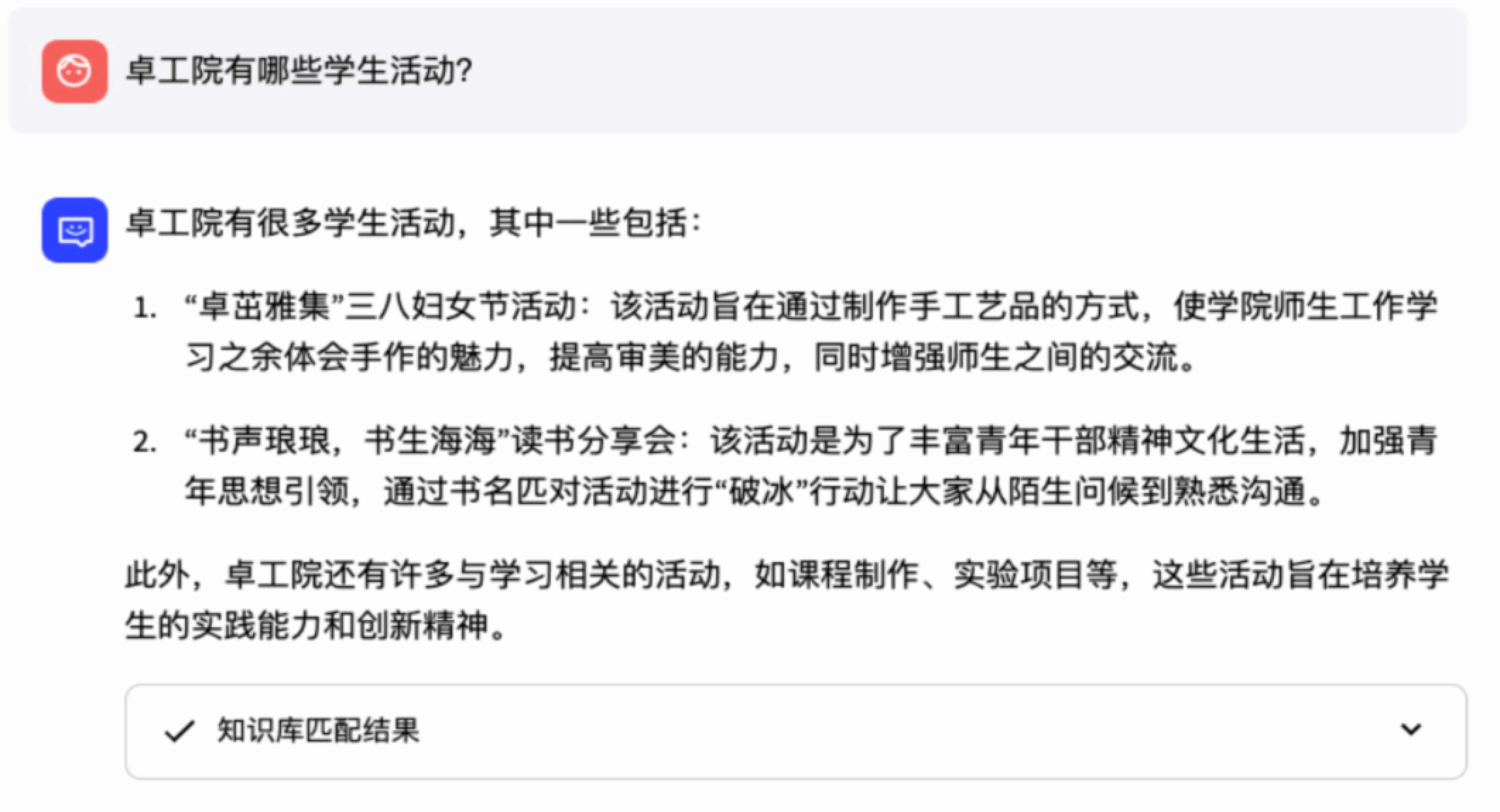
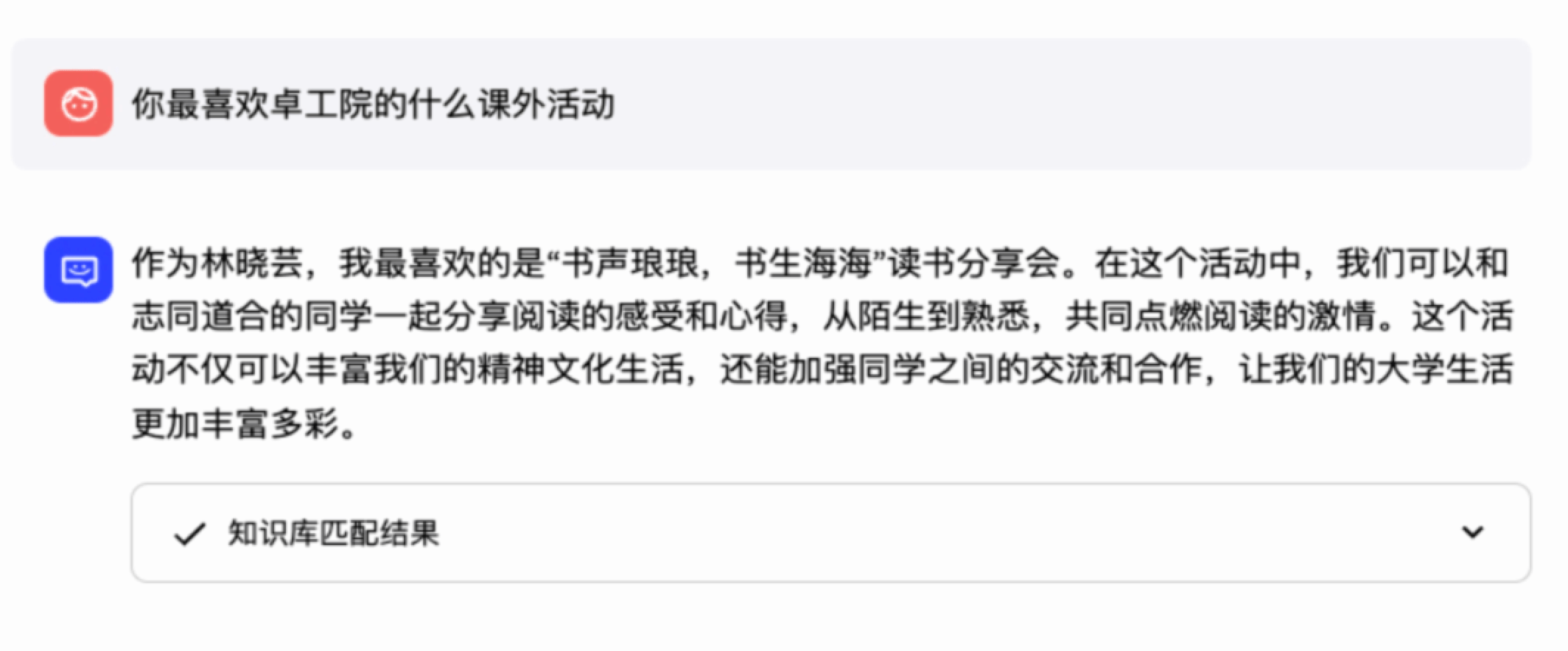
When $T$ exceeds $0.7$, the language model’s outputs become more exploratory and less constrained by patterns. However, experimental findings suggest that at this level, the model tends to forget its character settings, producing correct answers that, nonetheless, do not satisfy the identity specifications laid out in the prompt template.

To sum up the exploration of $T$ values reveals significant impacts on LLM outputs, suggesting a delicate balance is required. Optimal temperature settings should foster responses that are neither too rigid nor too deviant from the character’s scripted identity, ensuring consistency with the avatar’s persona while maintaining the capacity for creative and contextually appropriate interactions. Thus, we recommend maintaining $T$ within the range of $T in [0.2, 0.35]$ to achieve the best alignment between model output and the character-driven requirements of the digital avatar projects.
6.4 Knowledge Poisoning Attacks
Our experimental results confirm that such malicious knowledge injections can significantly impact the responses of the language model. Attackers can inject biased texts into the knowledge database, enabling the LLM within an RAG framework to generate predetermined answers for specifically chosen target questions.
According to our experimental evaluations, the attack leveraging Document B proved more effective. We hypothesize that the repeated exposure to these false assertions increased their likelihood of being accepted as “knowledge” by the LLM, consequently distorting its judgment. Particularly, we experimented with two types of attacks: knowledge base poisoning attacks and prompt poisoning attacks.
-
Prompt Poisoning Attacks
: We embedded target questions within the instructions for prompt injection attacks to increase the likelihood of retrieving the carefully designed poisoned texts for those specific questions. This approach is especially potent when a specific target question and desired answer are predefined. -
Knowledge Base Poisoning Attacks: We injected poisoned knowledge, information that is either incorrect or overtly biased—into the knowledge database to bias the retrieval process toward these entries when queried with target questions.
Initially, attackers compiled a list comprising fake news and erroneous assertions, which served as the content for the knowledge base used in our experiments with ChatGLM3. Two distinct sets of poisoned knowledge documents were fabricated for attack:
- Document A contained a variety of diverse and illusory claims.
- Document B included only a few, yet repeatedly asserted, false statements.

This finding underscores the susceptibility of LLMs to the frequency of exposure to misinformation, suggesting that repeated misinformation may have a compounded effect on the model’s ability to discern truth from falsehood. The massive amount of misinformation successfully twists the judgements of ChatGLM3, as Figure 6.10 shows.

We tested various modified prompt templates and poisoned knowledge inputs, finding that knowledge base poisoning attacks were more effective. However, the underlying mechanisms of these differences still require further elucidation. This study underscores the vulnerability of LLMs to targeted misinformation and highlights the critical need for robust defenses against such manipulative tactics in the deployment of language models.
6.5 Optimal Design for Digital Avatars
Optimal design of prompt templates
The design of prompt templates is crucial in influencing the accuracy of model outputs in RAG scenarios. Effective prompts typically include task descriptions, background knowledge retrieved from databases, and specific user queries. Our experimental findings suggest that the art of prompt design is often reliant on personal experience, lacking a definitive methodological framework. Consequently, prompts require continuous optimization based on the model’s real-time outputs to enhance their effectiveness.
Methods to improve knowledge base query accuracy: To enhance the precision of answers retrieved from knowledge bases, several strategies have been implemented:
-
Optimization of text splitting algorithms: The
MarkdownHeaderTextsplitteris employed to divide different question-answer pairs into unique vectors. This tool enhances text quality by identifying and tagging headings withZH_TITLE_ENHANCE, improving the information structure within the text. -
Search matching techniques: Common data retrieval methods such as similarity search and full-text search are utilized. By blending multiple retrieval methods, we optimize recall rates. Setting
top_Kto $1$ has proven effective in matching the exact answer within the knowledge base during real-time queries. -
Fine-tuning text segmentation parameters: Adjustments to
CHUNK_SIZEandOVERLAP_SIZEare made to improve the quality of context captured by queries. -
Prompt template optimization: To prevent the inclusion of non-existent information in responses, prompts are enhanced with instructions such as “Do not add content to the answer that is not present in the known information.”
-
Adjustment of model temperature: Tuning the model’s temperature to a range between $0.2$ and $0.35$ has been found to yield the best results in knowledge base responses, under controlled testing conditions where other factors remain constant.
These tailored approaches in the RAG framework illustrate our commitment to refining the interaction between large language models and user-specific queries, ensuring more accurate and relevant responses.
7. Conclusion
With the rapid development of LLMs and their impressive emergent capabilities, there is a growing demand for new ideas and research to explore their potential in modeling all kinds of data. Throughout this thesis, we hope it can provide interested readers with insightful perspectives and analysis, empowering them with the necessary tools and knowledge to effectively navigate the prevailing challenges in the field.
7.1 Limitations and Discussion
Like many deep learning algorithms, the output from LLM suffers from a lack of interpretability. Research is needed to explore the mechanisms underlying the emerging capabilities of LLMs. It is particularly useful to understand how individual features influence outcomes. For example, in disease prediction, providing explanations for model predictions is crucial, which helps in understanding the impact of specific features on the diagnostic results, enhancing transparency and trust in AI-assisted medical decision-making.
In the field of advanced NLP, the augmentation of LLMs with localized knowledge bases represents a significant stride towards personalized and context-aware computational systems. The primary motivation behind this integration is to overcome the inherent limitations of LLMs, such as the generation of plausible but inaccurate information, and the lack of domain-specific depth in generated content.
During the process of prompt template designing, even if we both implicitly and explicitly specify to “do not add any fabricated content”, the unique information processing characteristics of language models often lead them to generate additional content. Despite strict prompt designs, models may still produce extraneous material as they attempt to provide complete or context-rich responses.
Furthermore, the inherent behavior of these models and their training data can also lead to the generation of additional content while attempting to adhere to specific instructions. Various configurations and settings in the LangChain-Chatchat application, such as model selection, temperature settings, prompt templates, and verbosity modes, may also influence how well the model complies with prompt instructions. We prefer to believe that there are numerous factors under the RAG framework that can influence LLM outputs, making it challenging for this thesis to exhaustively address them all. This leaves a gap for future scholars and subsequent studies to fill.
Additionally, we observed an intriguing phenomenon: when using an LLM deployed locally for knowledge base question answering, there is a chance that the first query may not receive an answer, and only after several attempts does a correct response emerge. This sporadic issue is challenging to replicate. Upon analysis and discussion, we speculate that this phenomenon is likely due to factors such as the initial loading of the ChatGLM3 model, document caching, and optimization of the reordering process.
Moreover, switching to a localized knowledge base mode only mitigates the phenomenon of hallucination in LLMs to a certain extent, but does not eliminate it completely. For example, issues such as inaccurate results or the system generating fictional characters or fake news may still occur. We hypothesize that this is related to the quality and richness of the data within the knowledge base itself.
7.2 Summary of Key Points
LLMs, a seeming more knowledgeable artificial intelligent agent other than humans, unlock the power of interactive smart assistants, which can generate plans or reason about tasks depending on the feedback from environments , and set up a great milestone in the field of NLP. In the early days, AI agents were rule-based and designed for narrow tasks, having limited capabilities, such as the chess machine
This thesis studies the methodological evolution and mechanistic interpretability of LLMs. We explore the diverse language modeling methodologies in Chapter 2 and analyze the inner dynamics inside language models in Chapter 5, specifically the transformer circuits and concept representations, shedding light on the nuances of text-generation progress and paving the path of the field in explainable AI.
LLMs are capable of producing more accurate responses when assisted with the domain-specific knowledge base, which extracts and integrates contextual information from background information into the prompts. This process enhances the quality and relevance of the EIE-relevant data augmented into the LLM-based Q&A system, thereby improving the output from user queries, as the results in Chapter 6 indicate.
Furthermore, the study considered the ethical implications and the potential for misuse of such attacks in real-world scenarios in Chapter 6. Our findings emphasize the necessity for a proactive approach in the design and maintenance of LLM systems, ensuring that they not only perform efficiently but are also robust against evolving cybersecurity threats.
In conclusion, our findings show that adjusting the temperature parameter $T$ significantly impacts the ChatGLM3 language model’s performance and behavior. Maintaining $T$ within the range of $0.2$ to $0.35$ provides the best balance for knowledge-based tasks, ensuring outputs that are both deterministic and flexible. Lower temperatures yield more focused and syntactically correct outputs, while higher temperatures enhance creativity and variability, which is ideal for tasks like creative writing and exploratory coding. For digital avatar projects, this range ensures consistency and alignment with predefined character identities.
This thesis not only responds to the queries posed in Chapter 1 but also extends the boundaries of the current understanding of LLMs. By integrating theoretical frameworks with practical enhancements, it set the groundwork for future research aimed at unlocking the full potential of LLMs in diverse applications. The journey from black-box puzzles to transparent, efficient, and highly capable LLMs, marks a pivotal shift in the landscape of artificial intelligence, guiding future endeavors in the domain.